19 - Series - convergence tests

Where we left off last time

Where did we leave off last time and where were we going? What are some more convergence tests we can use for series?

• Recap: Last time we were talking about series which are special kinds of sequences. A series is a sequence of partial sums. Last time we asked ourselves how we can tell whether or not a series converges. So what if you have a series like

  $$\sum\frac{1}{n^2}=1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\cdots$$

  We should look at this as a sequence of partial sums:

  $$\sum\frac{1}{n^2}=\underbrace{\underbrace{\underbrace{\underbrace{1}_{s_1}+\frac{1}{4}}_{s_2}+\frac{1}{9}}_{s_3}+\frac{1}{16}}_{s_4}+\cdots$$

  or also (but less useful in terms of appearance)

  $$\{1,\tfrac{5}{4},\tfrac{49}{36},\tfrac{205}{144},\ldots\}.$$

  And we wanted to know whether or not the sequence of partial sums converged. And what are some of the things we talked about last time? How did we test for convergence of a series? We can compare the given series to another series we know something about. The comparison test tells us to compare term by term to see if it's dominate in some way. What would we compare to, for instance? The geometric series is a classic series to look at when comparing things. We gave conditions for which $\Sigma\frac{1}{n^p}$ converges, and we did this by making use of a clever comparison. The comparison test itself has its roots in what? The Cauchy criterion for sequences, when applied to series, gives a Cauchy criterion for series. We want to show that if the tails are bounded then we are in very good shape.

• Note about root and ratio tests that follow: In what follows, the "high school" definitions of these tests will be given first, and then these will be modified appropriately based on our new knowledge.

• The root test (high school; see [9]): We have three cases:

  1. If $\lim_{n\to\infty}\sqrt[n]{|a_n|}=L<1$, then the series $\sum_{n=1}^\infty a_n$ is absolutely convergent and therefore convergent.
  2. If $\lim_{n\to\infty}\sqrt[n]{|a_n|}=L>1$ or $\lim_{n\to\infty}\sqrt[n]{|a_n|}=\infty$, then the series $\sum_{n=1}^\infty a_n$ is divergent.
  3. If $\lim_{n\to\infty}\sqrt[n]{|a_n|}=1$, then the root test is inconclusive.

• The root test: Given $\Sigma a_n$, let $\alpha=\limsup_{n\to\infty}\sqrt[n]{|a_n|}$. We have three cases:

  1. If $\alpha<1$, then $\Sigma a_n$ converges.

  Proof. If $\alpha<1$, choose $\beta$ such that $\alpha<\beta<1$. If $\alpha=\limsup_{n\to\infty}\sqrt[n]{|a_n|}<\beta<1$, then that means there is a point in the sequence beyond which all the terms are smaller than $\beta$. Thus, there exists $N$ such that $n\geq N$ implies that $\sqrt[n]{|a_n|}<\beta$ (by the definition of $\limsup$). So now we are going to compare with the geometric series whose ratio is $\beta$. But what does $\sqrt[n]{|a_n|}<\beta$ really mean and why is it useful? It's the same as saying that $|a_n|<\beta^n$ for $n\geq N$. Well, we know $\Sigma\beta^n$ converges, so $\Sigma |a_n|$ converges also. So then why does $\Sigma a_n$ converge also? By the comparison test. So this concludes the proof here.

  2. If $\alpha>1$, then $\Sigma a_n$ diverges.

  Proof. If $\alpha>1$, then what goes wrong here? Well, if $\alpha>1$, then we have $\alpha=\limsup_{n\to\infty}\sqrt[n]{|a_n|}>1$ by definition, and this means that there is a subsequence that converges to something bigger than 1. But if the subsequence converges to something bigger than 1, then that basically means the terms do not go to zero. That's the intuition here.

  There exists a sequence $\{n_k\}$ such that $\sqrt[n_k]{|a_{n_k}|}\to\alpha>1$. So what? Well, then $|a_{n_k}|>1$ for infinitely many terms so the terms do not go to zero and the series diverges.

  3. If $\alpha=1$, then the test gives no information.

  Proof. If $\alpha=1$, then note that $\Sigma\frac{1}{n}$ diverges but $\Sigma\frac{1}{n^2}$ converges. Since $\alpha=1$ in both cases, we realize the test is inconclusive.

  In high school you let $\alpha=\lim_{n\to\infty}\sqrt[n]{|a_n|}$, but this is not the best way of stating this because the limit may not exist. But here's something that always exists: the limit may not exist but the $\limsup$ always exists. Or it might be possibly infinite, but the point is that it can be calculated in the extended reals.

  In terms of motivation, we realize that when we put $\alpha=\limsup_{n\to\infty}\sqrt[n]{|a_n|}$ that $a_n$ is kind of like $\alpha^n$. So the series $\Sigma a_n$ kind of looks like the geometric series in some way. This was the motivation for comparing $\Sigma a_n$ to the geometric series. (Many proofs will involve comparisons with the geometric series.) As a side note, the root test is way more powerful than the ratio test, but the ratio test is often easier to use. The reason the ratio test is not always so powerful is because there are sequences that converge but for which the ratio we look at does not give much information. So you might look at a sequence like

  $$1,1,\tfrac{1}{2},\tfrac{1}{2},\tfrac{1}{4},\tfrac{1}{4},\tfrac{1}{8},\tfrac{1}{8},\ldots$$

  Well, the successive ratios will be 1, $\frac{1}{2}$, 1, $\frac{1}{2}$, etc. The ratio test here is not going to tell me much. That's why the ratio test is not always so powerful.

• The ratio test (high school; see [9]): We have three cases:

  1. If $\lim_{n\to\infty}\Bigl|\frac{a_{n+1}}{a_n}\Bigr|=L<1$, then the series $\sum_{n=1}^\infty a_n$ is absolutely convergent and therefore convergent.

  2. If $\lim_{n\to\infty}\Bigl|\frac{a_{n+1}}{a_n}\Bigr|=L>1$ or $\lim_{n\to\infty}\Bigl|\frac{a_{n+1}}{a_n}\Bigr|=\infty$, then the series $\sum_{n=1}^\infty a_n$ is divergent.

  3. If $\lim_{n\to\infty}\Bigl|\frac{a_{n+1}}{a_n}\Bigr|=1$, then the ratio test is inconclusive.

• The ratio test: The series $\Sigma a_n$

  1. converges if $\displaystyle\limsup_{n\to\infty}\biggl|\frac{a_{n+1}}{a_n}\biggr|<1$, and

  Proof. If $\limsup_{n\to\infty}\Bigl|\frac{a_{n+1}}{a_n}\Bigr|<1$, then once again we have $\Bigl|\frac{a_{n+1}}{a_n}\Bigr|<\beta<1$ for some $\beta$ with $n_0\geq N$. How does this help me compare? And what are we going to compare to? The geometric series again! Well, from $\Bigl|\frac{a_{n+1}}{a_n}\Bigr|<\beta$ we can make the connection $|a_{n+1}|<\beta|a_n|$ so each time we're introducing at most a factor of $\beta$. What does this mean? We could keep going:

  $$|a_{n+1}|<\beta|a_n|<\beta^2|a_{n-1}|<\beta^3|a_{n-2}|<\cdots$$

  What you find eventually is that you can go as far back as you want, and you just introduce a new $\beta$ each time. So what you could see is (by the same argument)

  $$|a_{N+k}|<\cdots<\beta^k |a_N|.$$

  So let's start at $a_N$ and look at the tail: $\sum_{k=0}^\infty a_{N+k}\leq a_N\sum \beta^k$, but this latter sum converges thus bounding the tail. And this is enough to give us the convergence of our series.

  2. diverges if $\displaystyle\biggl|\frac{a_{n+1}}{a_n}\biggr|\geq1$ for all $n\geq n_0$, where $n_0$ is some fixed positive integer.

  Proof. For divergence, we can see that the terms do not go to 0.

Power series

What are power series and what are some observations we can make about them?

• Motivation: One of the most important series you will encounter is a power series.

• Power series (definition): What is a power series? Well, a series is basically just a sum of a bunch of numbers. A power series might involve variables. Given a sequence $\{c_n\}$ of complex numbers, the series

  $$\sum_{n=0}^\infty c_nz^n=c_0+c_1z+c_2z^2+\cdots$$

  The above is a power series. It's a series of powers of $z$, and $z$ here you think of some complex variable in $\C$.

• Natural questions: Given a bunch of constants $c_i$, a natural question is to ask for what values of $z$ does the power series converge? The nice answer to this question is that we can use our knowledge of convergence tests to answer this.

• Convergence of power series: If $\alpha=\limsup_{n\to\infty}\sqrt[n]{|c_n|}$, let $R=\frac{1}{\alpha}$. Then $\Sigma c_nz^n$ converges if $|z|<R$, and diverges if $|z|>R$. The number $R$ is called the radius of convergence.

  The surprise is the set of all places where the series $\sum_{n=0}^\infty c_nz^n$ converges actually forms a disk. It is a circle in the plane and is centered around 0 in this case. It's amazing it's a circle, but you can see where it comes from because the proof involves the root test. In this case, with $a_n=c_nz^n$, we have $\sqrt[n]{|a_n|}=|z|\cdot\sqrt[n]{|c_n|}$. What you're hoping is that the $\limsup$ of this stuff is less than 1 (we will apply the root test). So we'll write

  $$\limsup_{n\to\infty}\sqrt[n]{|a_n|}=|z|\limsup_{n\to\infty}\sqrt[n]{|c_n|}=|z|\cdot\alpha<1.$$

  Thus, here we're really looking at just comparing $|z|$ with $\frac{1}{\alpha}$. That's where the $R$ comes from. We're just using the root test. This is the proof idea.

Combining sequences

How might we combine sequences in a meaningful way?

• Motivating question: Given two sequences $\{a_n\}$ and $\{b_n\}$, we may be interested in how to combine these sequences and study them. What might we be able to say about the sum of these sequences? Can we say anything meaningful about $\Sigma a_nb_n$?

• Summation by parts: Let

  $$A_n=\sum_{k=0}^n a_k$$

  for $n\geq0$, and set $A_{-1}=0$. Then

  $$\sum_{n=p}^q a_nb_n=\sum_{n=p}^{q-1} A_n(b_n-b_{n+1})+A_qb_q-A_{p-1}b_p.$$

  How is this like integration by parts (from which you've seen in early calculus classes)? What are some general features of this formula that remind you of integration by parts? Integration by parts says something loosely along the lines of

  $$\int u\,dv=uv-\int v\,du.$$

  Integrals are like sums. So if we want to integrate $u\,dv$ here, then what's playing the role of $u$ and $dv$ here, respectively? What's playing the role of the integral here? The sum, $\Sigma$. What's playing the role of $u$ and $dv$ here? We have $A_n$ playing the role of $v$, and if we let $A_n$ be the partial sums (as it is defined above), then the change in $A_n$ is little $a$ at every step.

  So we basically have $A=v$ and $a=dv$. Then we have $b=u$ and $b_n-b_{n+1}=du$. So we almost get

  $$\sum_{n=p}^q a_nb_n=\sum_{n=p}^{q-1} A_n(b_n-b_{n+1})+A_qb_q-A_{p-1}b_p$$

  is basically

  $$\int u\,dv = \int v\,du-vu.$$

  Why do we have the two terms $A_qb_q-A_{p-1}b_p$ at the end of the summation formula? We have to evaluate at the endpoints. So we have

  $$\int_p^q dv\,u = \int_p^{-1} v\,du -vu|_p^{q}=\int_p^q dv\,u = -\int_p^{\textcircled{-1}} v\,du +vu|_p^{\textcircled{q}},$$

  where circles have been added to show where things are slightly off. The upshot is that integration by parts and summation by parts are really the same concept. Showing why summation by parts holds for sequences actually gives you a visual for integration by parts in the discrete case. Down the road, we'll see that summation is actually integration with respect to a certain integrator. So summation can actually be thought of as a special case of integration, where you're integrating over a discrete set.

• Summation by parts (proof idea): The algebraic proof gives no insight whatsoever. This is the geometric idea. Imagine a square that's broken up into little pieces(here we will just consider 4 breaks in both directions):

  

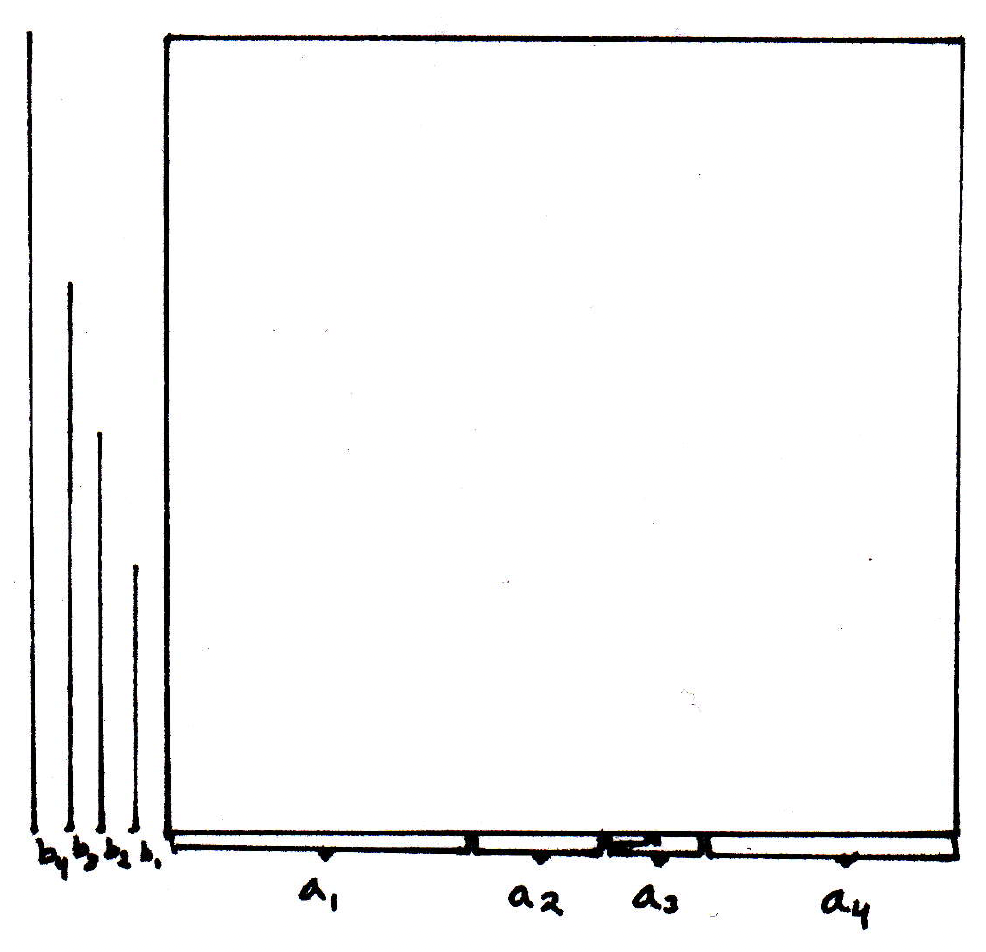
  Then we can visualize $\Sigma a_nb_n$ in the following way: We get the following for the first summand (the areas are the rectangles):

  

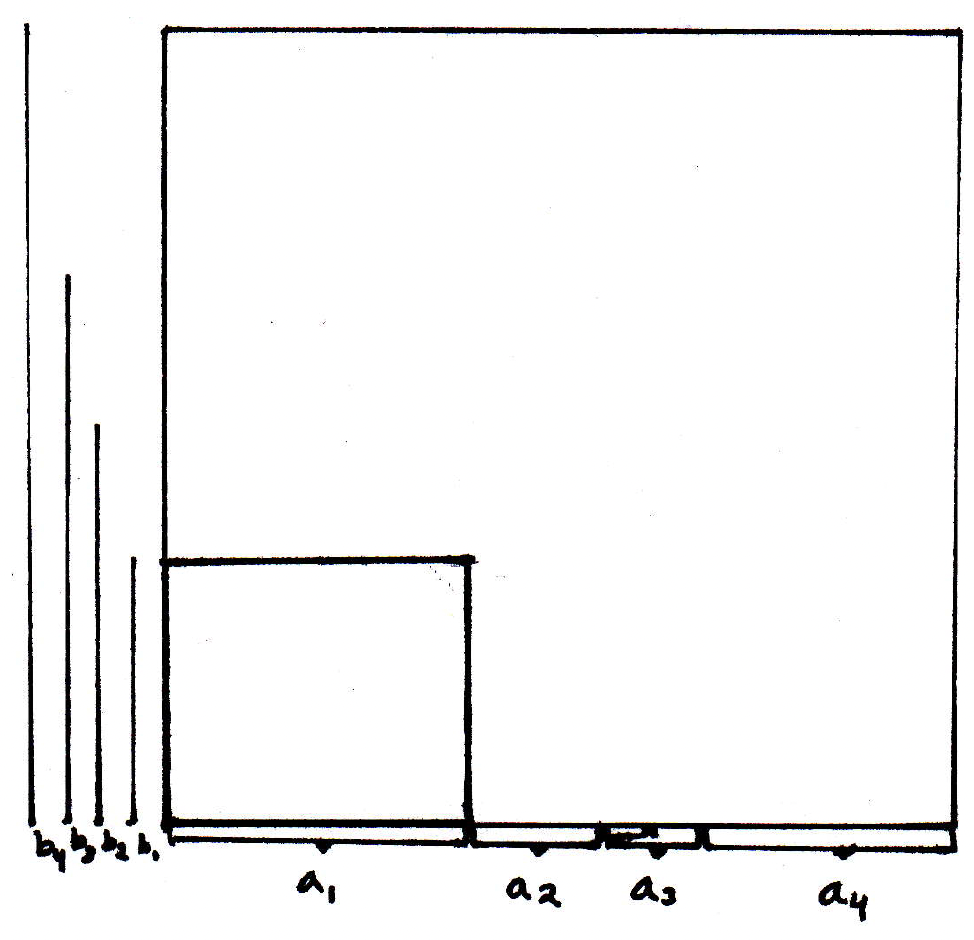
  The second summand:

  

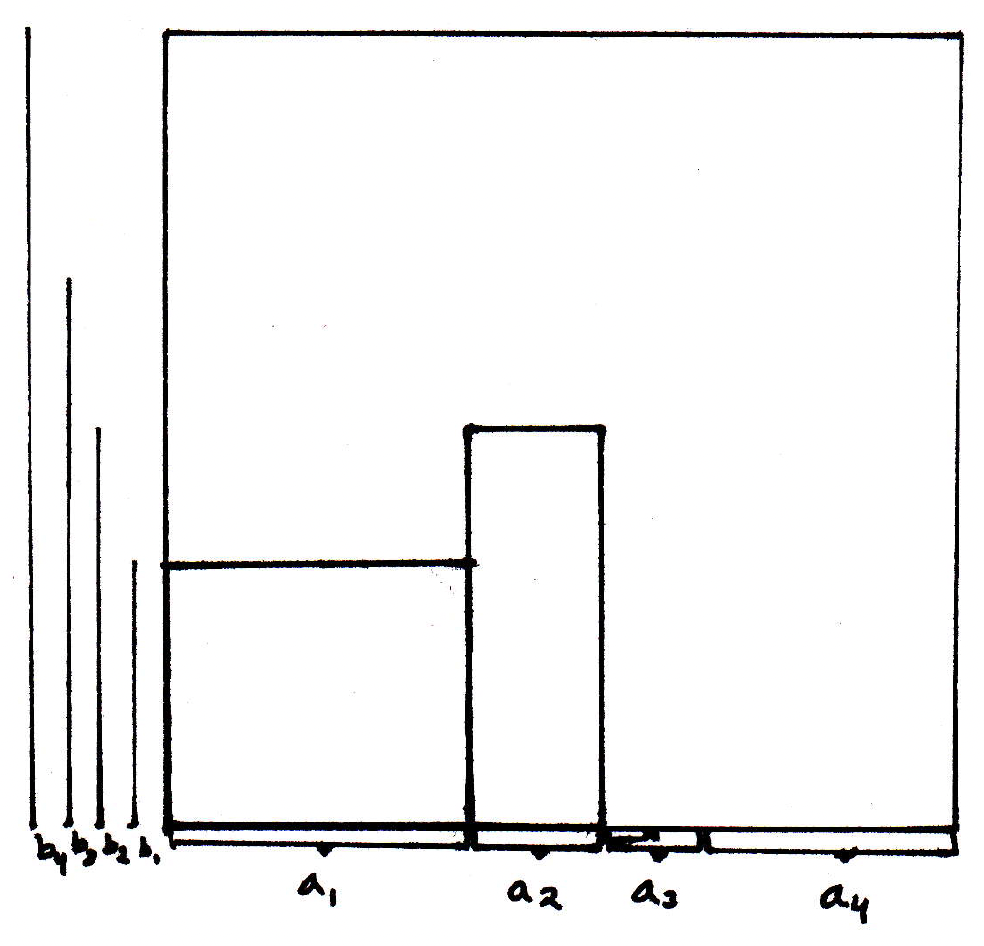
  The third summand:

  

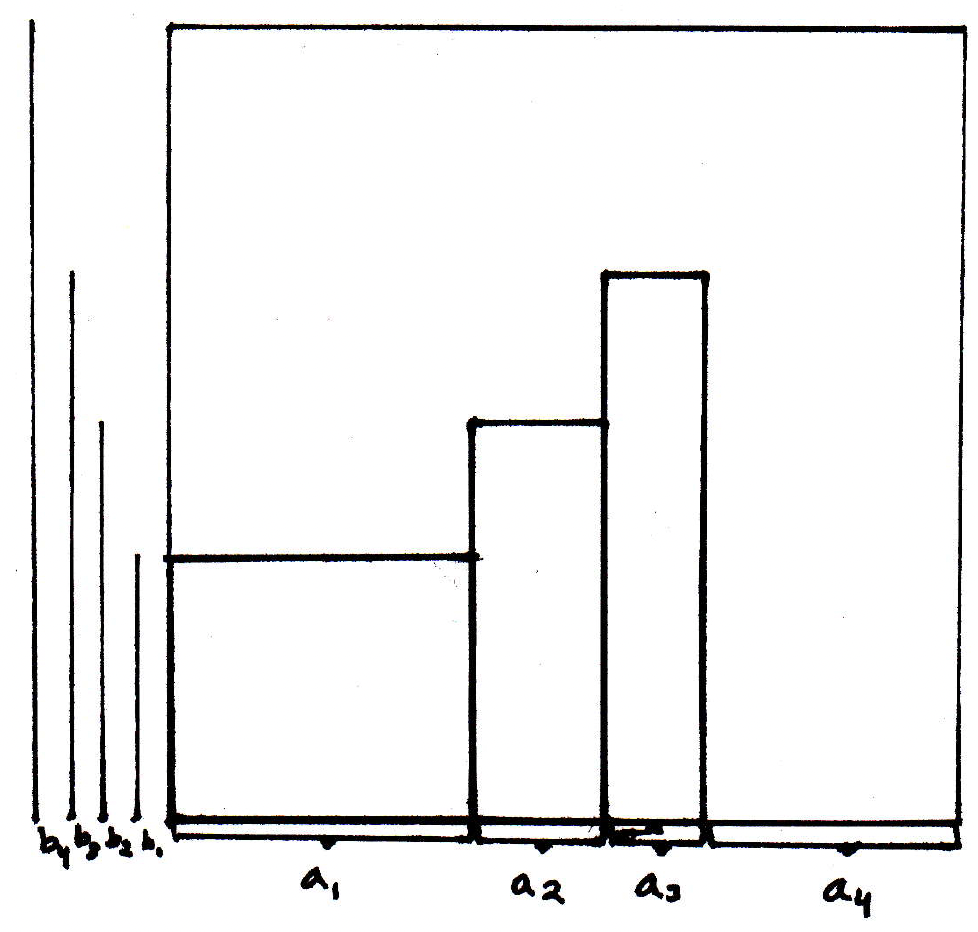
  The fourth summand:

  

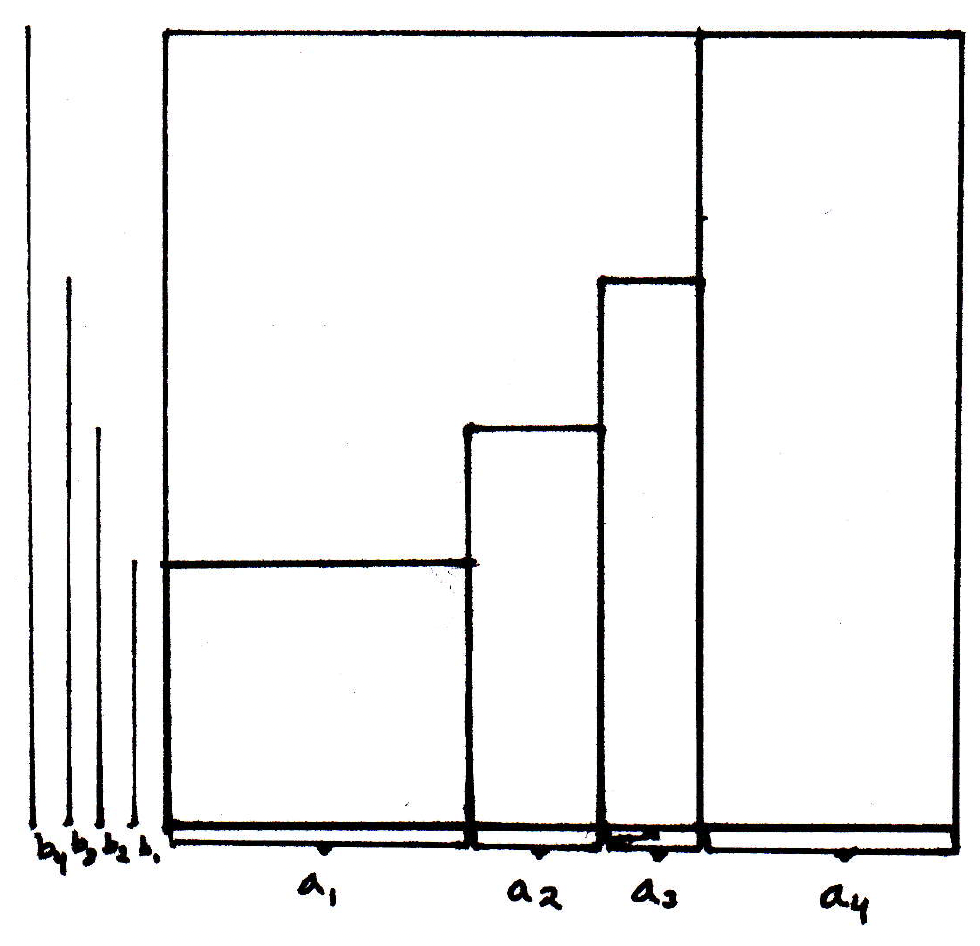
  Now we can see the relationship with integration by parts. If $a=dv$ and $b=u$, then integration by parts says to find the areas of the rectangles in question, we should take the whole area of the box and subtract out the sum of the areas of the dashed rectangles below:

  

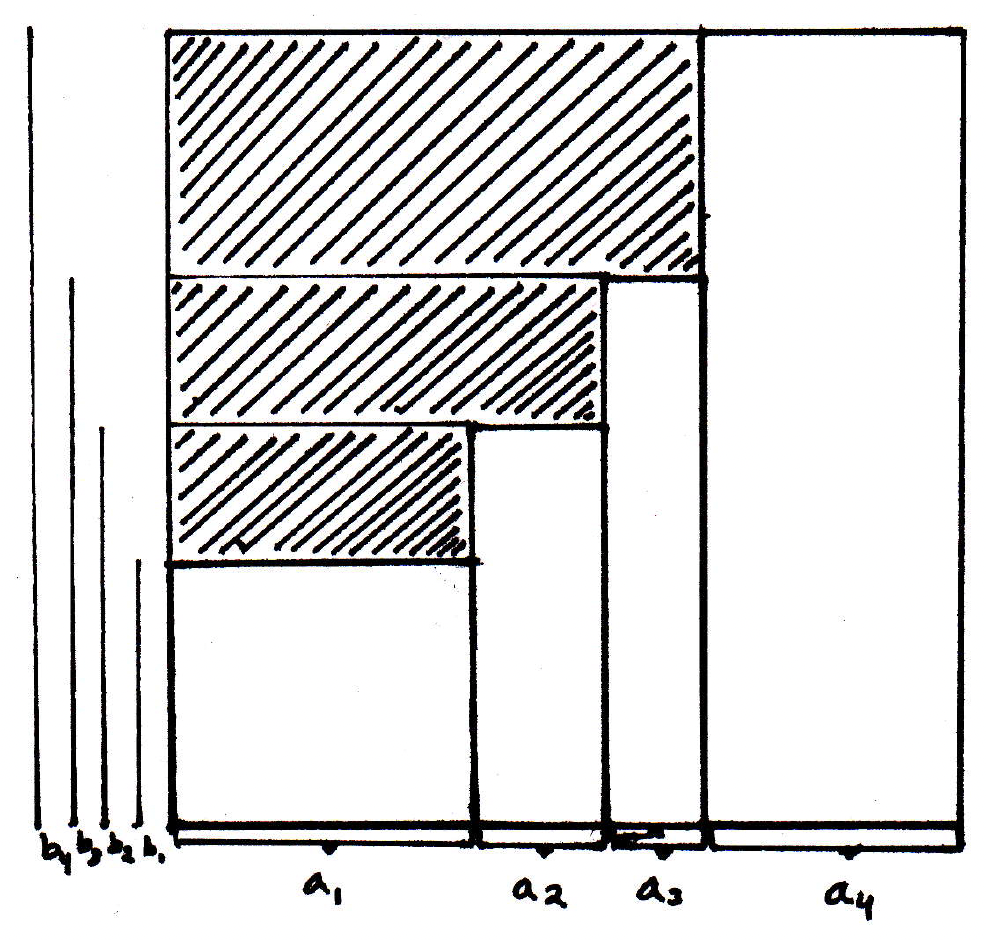
  Remember the formulation for integration by parts:

  $$\int u\,dv=uv-\int v\,du.$$

  We can see the relationship. For the algebraic proof, see [17]. This leads us to the following theorem.

• Theorem (see [17]): Suppose

  1. the partial sums $A_n$ of $\Sigma a_n$ form a bounded sequence;
  2. $b_0\geq b_1\geq b_2\geq\cdots$;
  3. $\lim_{n\to0}b_n=0$.

  Then $\Sigma a_nb_n$ converges.

  Basically this is saying that of the partial sums involved in $\Sigma a_nb_n$ are bounded and $b_n\to0$, then we are in good shape.

• Proof of theorem (idea): Suppose $|A_n|\leq M$, $b_0\geq b_1\geq b_2\geq\cdots$, and $b_n\to0$. Fix $\epsilon>0$. Then there exists $N$ such that $b_N\leq\frac{\epsilon}{2M}$. Recalling

  $$\sum_{n=p}^q a_nb_n=\sum_{n=p}^{q-1} A_n(b_n-b_{n+1})+A_qb_q-A_{p-1}b_p,$$

  we can bound this in a meaningful way for $q\geq p\geq N$:

  $$\begin{align*} \biggl|\sum_{n=p}^q a_nb_n\biggr| &= \biggl|\sum_{n=p}^{q-1}A_n(b_n-b_{n+1})+A_qb_q-A_{p-1}b_p\biggr|\\[1em] &\leq M\biggl|\sum_{n=p}^{q-1}(b_n-b_{n+1})+b_q+b_p\\[1em] &= 2Mb_p\\[1em] &\leq 2Mb_N\\[1em] &\leq \epsilon. \end{align*}$$

  We've just bounded the tails by $\epsilon$ which is what we need for the Cauchy criterion.

• Example: Suppose $|c_1|\geq|c_2|\geq\cdots$ and that the $c_i$ alternate in sign and go to zero. Then the claim is that $\Sigma c_n$ converges. This is the alternating series test. The proof follows from our proof for the theorem above with $a_n=(-1)^{n+1}$ (its partial sums are basically just 1s and 0s so it's bounded) and $b_n=|c_n|$.

• Sums of series: We have $\Sigma a_n+\Sigma b_n=\Sigma(a_n+b_n)$.

• Products of series: It's not defined quite as you would think, namely $\Sigma a_n\cdot\Sigma b_n=\Sigma a_nb_n$. Let's see if we can motivate why this might be the case and where the generally accepted definition comes from.

  The motivation actually comes from power series. With power series we might have a series that starts off like

  $$a_0+a_1z+a_2z^2+\cdots$$

  and another one like

  $$b_0+b_1z+b_2z^2+\cdots.$$

  If we consider the product

  $$(a_0+a_1z+a_2z^2+\cdots)(b_0+b_1z+b_2z^2+\cdots),$$

  how should one go about evaluating this? What would you get? What's the first term? We'd get

  $$(a_0b_0)+(a_1b_0+a_0b_1)z+(a_2b_0+a_1b_1+a_0b_2)z^2+\cdots.$$

  With this motivation, the following is how we define the product of two series: Given $\Sigma a_n$ and $\Sigma b_n$, we put

  $$c_n=\sum_{k=0}^{n}a_kb_{n-k},$$

  and we call $\Sigma c_n$ the product of the two given series.

• More motivation for product definition of series: Another reason the product of two series is defined the way it is and not what you might expect is that if

  $$A_n=\sum_{k=0}^n a_k \qquad\text{and}\qquad B_n=\sum_{k=0}^n b_k,$$

  and $A_n\to A$ and $B_n\to B$, then

  $$\sum_{n=p}^q a_nb_n$$

  will actually not converge to $AB$. So that would not be a good notion of a product. But the way we've defined our product of series does converge how you would want it to under certain conditions.

  Here's the problem: The sum $\Sigma c_n$ may not converge even if $\Sigma a_n$ and $\Sigma b_n$ do, but if $\Sigma a_n$ and $\Sigma b_n$ converge absolutely to $A$ and $B$, respectively, (we'll define what that means momentarily) then $\Sigma c_n$ converges to $AB$.

Absolute convergence

What is absolute convergence and why is it important?

• Idea: Absolute convergence is basically a kind of convergence where you look at absolute values.

• Absolute convergence (definition): The series $\Sigma a_n$ converges absolutely if $\Sigma |a_n|$ converges.

• Example involving absolute convergence: Consider the series

  $$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$$

  Does this converge? Yes, it's a sum of alternating terms that decreases and goes to 0. Does it converge absolutely? No, since its absolute series is going to be the harmonic series.

• Theorem: absolute convergence implies convergence: If $\Sigma a_n$ converges absolutely, then $\Sigma a_n$ converges.

  Why? If we're estimating the sum, then the Cauchy criterion tells us so look at the tail $|\sum_{k=n}^m a_k|$, but that's bounded by $\sum_{k=n}^m |a_k|$. Thus, we see that

  $$\biggl|\sum_{k=n}^m a_k\biggr|\leq\sum_{k=n}^m |a_k|,$$

  but $\sum_{k=n}^m |a_k|$ is the tail of the absolutely convergent series, and thus we know $\sum_{k=n}^m |a_k|$ is small by the Cauchy criterion for $\sum|a_k|$. So if we can make $\sum_{k=n}^m |a_k|$ small, then use the same $N$ for a given $\epsilon>0$ to make $|\sum_{k=n}^m a_k|$ small, and then you're in good shape.

Rearranging series

What are rearrangements of series and why are they important?

• Motivation: We've seen one place where absolute convergence might be important, namely when trying to look at the product of two series. Another situation where things might go really bad if a series does not converge absolutely has to do with rearranging the terms of a series. So if you take a series, then you might naturally ask what happens if you sum things in a different order? So suppose $\Sigma a_n=A$. If we rearrange the terms, must $\Sigma a_n$ still converge? No. If it does converge, then must it still converge to $A$? The answer to this is a big, resounding no as well. It will be informative to look at an example of where things can go bad.

  Consider the series mentioned previously, namely

  $$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots=\ln 2.$$

  But guess what? Not only would a rearrangement not necessarily converge to $\ln 2$, but we could get it to converge to any number you like. Seriously? How about $\pi$? This is a result due to Riemann (not the $\pi$-result): If $\Sigma a_n$ converges but not absolutely, then a rearrangement can have any limit you like. (It's really even worse than this; it can have any $\limsup$ or $\liminf$ that you like.) So it may not converge, but basically you can get it to do whatever you want. If $\Sigma a_n$ does converge absolutely, however, then all rearrangements have the same limit. This is an amazing fact; indeed, it is one of the main reasons why we care about absolute convergence.

  So let's see how we can get

  $$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$$

  to converge to $\pi$ by using a suitable rearrangement. Take a look at all of the odd terms. They are all positive. What can we say about the series of odd terms? It diverges. What about the even terms? They are all negative and diverge as well. So the positive and negative terms get as large positive or large negative as you like. The basic idea is this: We can start by summing the positive terms until we slightly overshoot $\pi$ and then start summing the negative terms until we slightly overshoot $\pi$ in the other direction. And we keep on doing this (so we'll get a series that converges to $\pi$):

  $$\underbrace{\underbrace{1+\tfrac{1}{3}+\tfrac{1}{5}+\tfrac{1}{7}+\cdots}_{>\pi}-\tfrac{1}{2}-\tfrac{1}{4}-\tfrac{1}{6}-\cdots}_{<\pi}+\cdots$$

  This is an amazing fact about rearrangements. If your series is not absolutely convergent, then you can use rearrangements to get it to do whatever you want.