10 - Relationship between open sets and closed sets

Where we left off last time

What happened last time? Where did we get to and where we going?

• Topology of the real line: We were developing some of the notions involved in the topology of the real line. In particular, we talked about open and closed sets, and we want to talk a bit about their relationship today.

• Open set: A set $E$ in a metric space $X$ is open if every point is an interior point, where by "interior point" we mean a point that has a neighborhood around it that is completely contained in $E$. Consider the following picture:

  

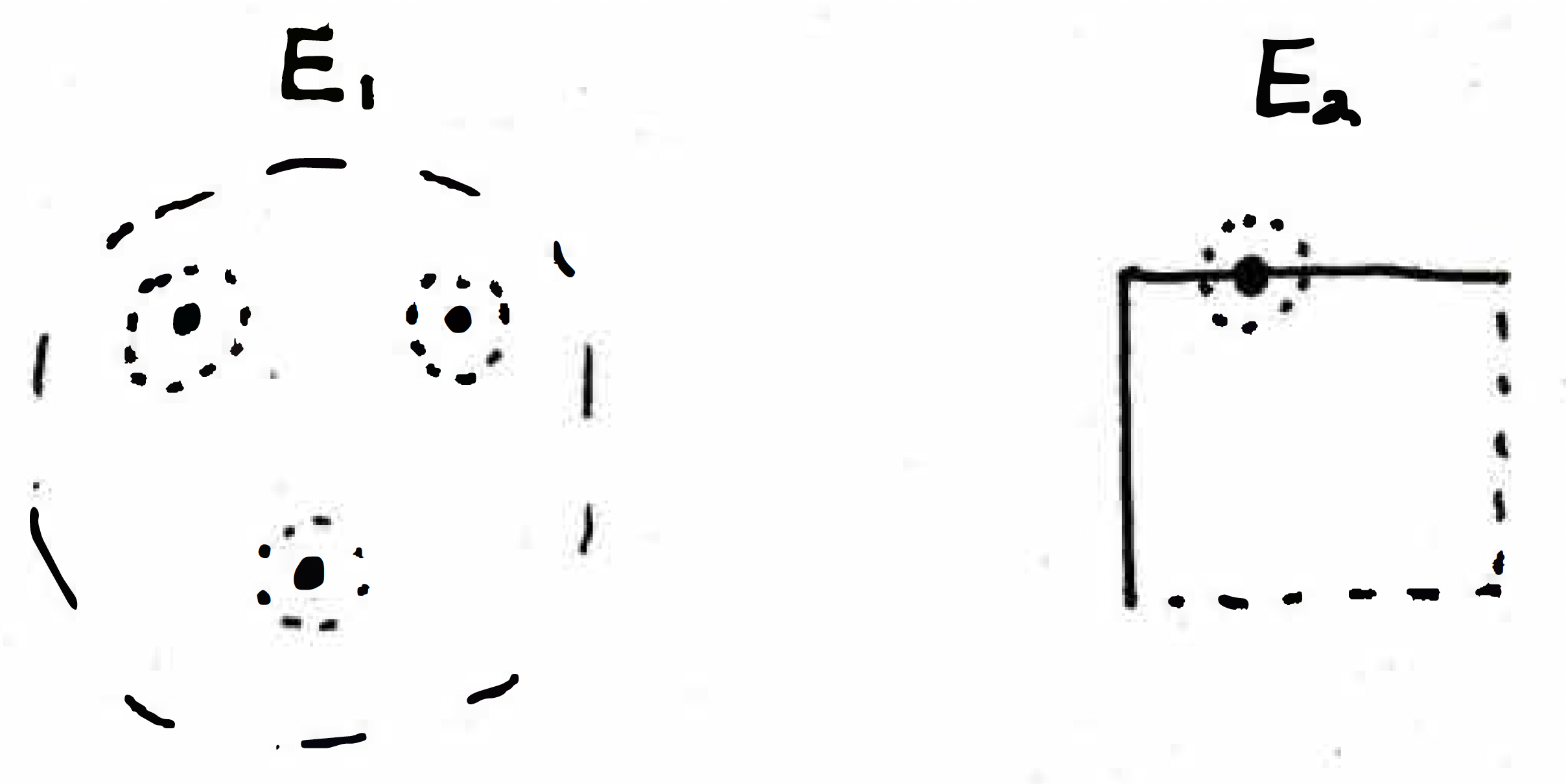
  It is clear that all three points illustrated in $E_1$ are interior points. There exists a neighborhood around each of these points such that the neighborhood is completely contained in $E_1$. Of course, the closer and closer we might get to the boundary, the smaller and smaller the neighborhood would have to get in order for the neighborhood to be completely contained in $E_1$. For the set $E_2$, the point on the boundary clearly poses a problem. No matter how small I make a neighborhood of this point, the neighborhood will never be completely contained in $E_2$. Thus, $E_2$ is not an open set. So why are open sets really important? We kind of alluded to that last time, but we were just making definitions.

• Importance of open sets: Why do we care so much about open sets? We're used to thinking of pictures in Euclidean space, but let's try to think a little more broadly. This could be any metric space. And really what I'm saying when I say that a set is open is that if I take any point $p$ then I can push it around a little bit and it still remains in the set $E$. So to be open means I can perturb points in $E$ and still have them stay within $E$. So an example might be to look at the set of all triples of points in the plane. Take three points in the plane. Are they collinear? Yes if they all lie on the same line, of course. Suppose we look at the set of all triples of points that are not collinear. Is such a set an open set? Intuitively yes because if three points are not collinear, then if perturb it is it not still not collinear? If you were really close to being collinear, then you may not be able to perturb it much but just a little bit. So that's one of the reasons why the concept of an open set is extremely important. It means you can push something around but it still remains in the set. Is that true of the point illustrated in $E_2$? No, if you push it around, then it may leave the set.

• Closed sets: What does it mean for a set to be closed? A set $K$ is closed if $K$ contains all of its limit points, where by "limit point" we mean a point $p$ of a set $S$ such that every deleted neighborhood of $p$ contains a point of $S$. Why do you think it's important for us to understand when a set is closed? What does it mean for a closed set to contain all its limit points? What's so important about have a set contain its limit points? Consider the following picture of a closed set $K$:

  

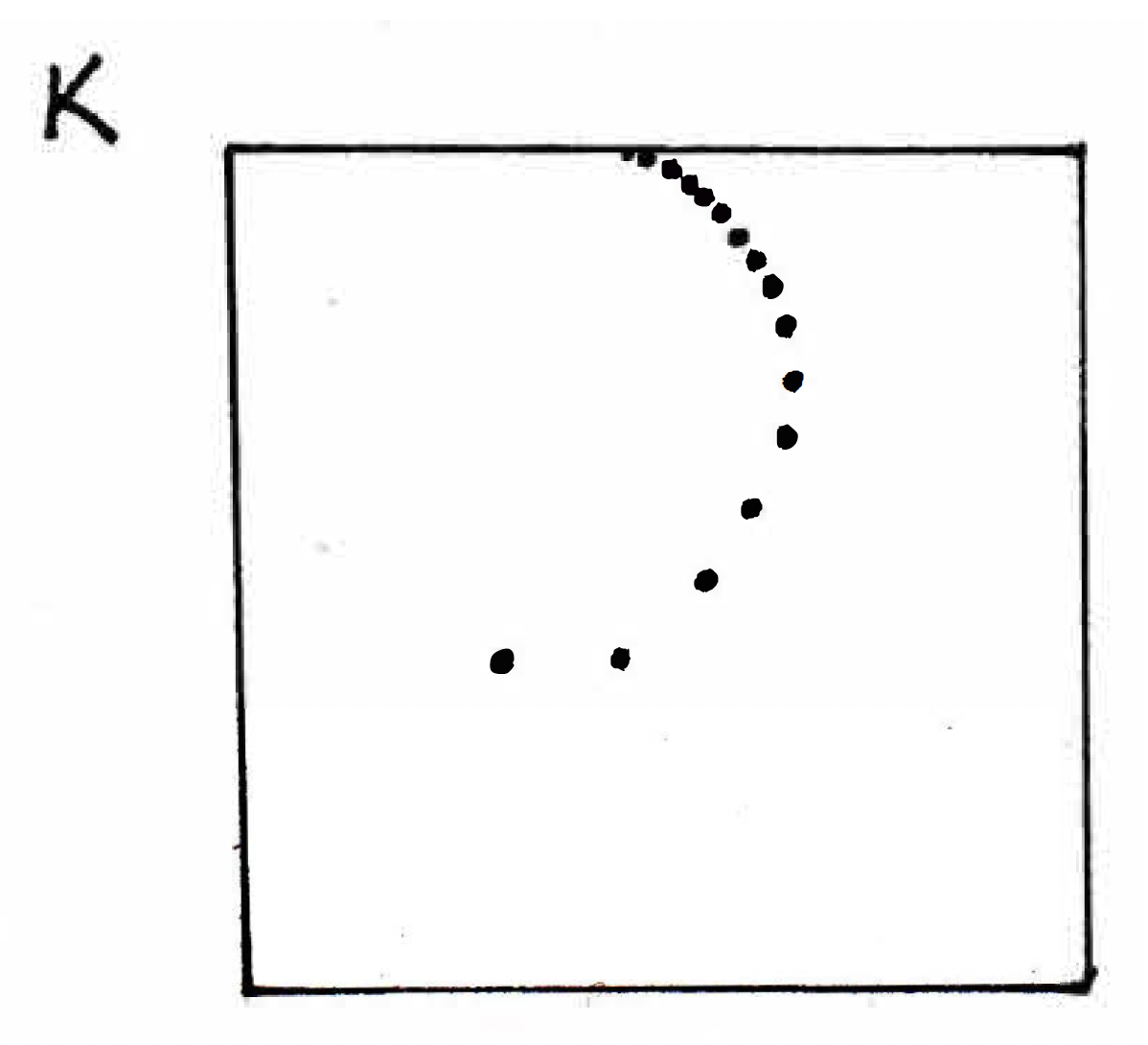
  It might be the case as we continue our exploration of metric spaces that maybe we'll have a sequence, and we will want to know whether or not it actually has a limit. And, if so, is that limit also in the set? The example above concerns points, but we could also be talking about functions (in engineering or physics you might be concerned with whether or not a sequence of functions has a limit — it could be some wave form of some signal). We have to define what it means to be a limit of a sequence, but I claim that's very closely related to the notion of a limit point of a set. So asking whether or not a set contains all of its limit points will be a very useful consideration in the not too distant future. This is just some motivation for these concepts and why we are studying them so carefully.

Closure of a set

What exactly is the closure of a set and why is it important?

• Closure of a set (definition): The closure of a set $A$ is $\overline{A}=A\cup A'$, where $A'$ denotes the set of limit points of $A$. Consider the sets $A_1$ and $A_2$ below.

  

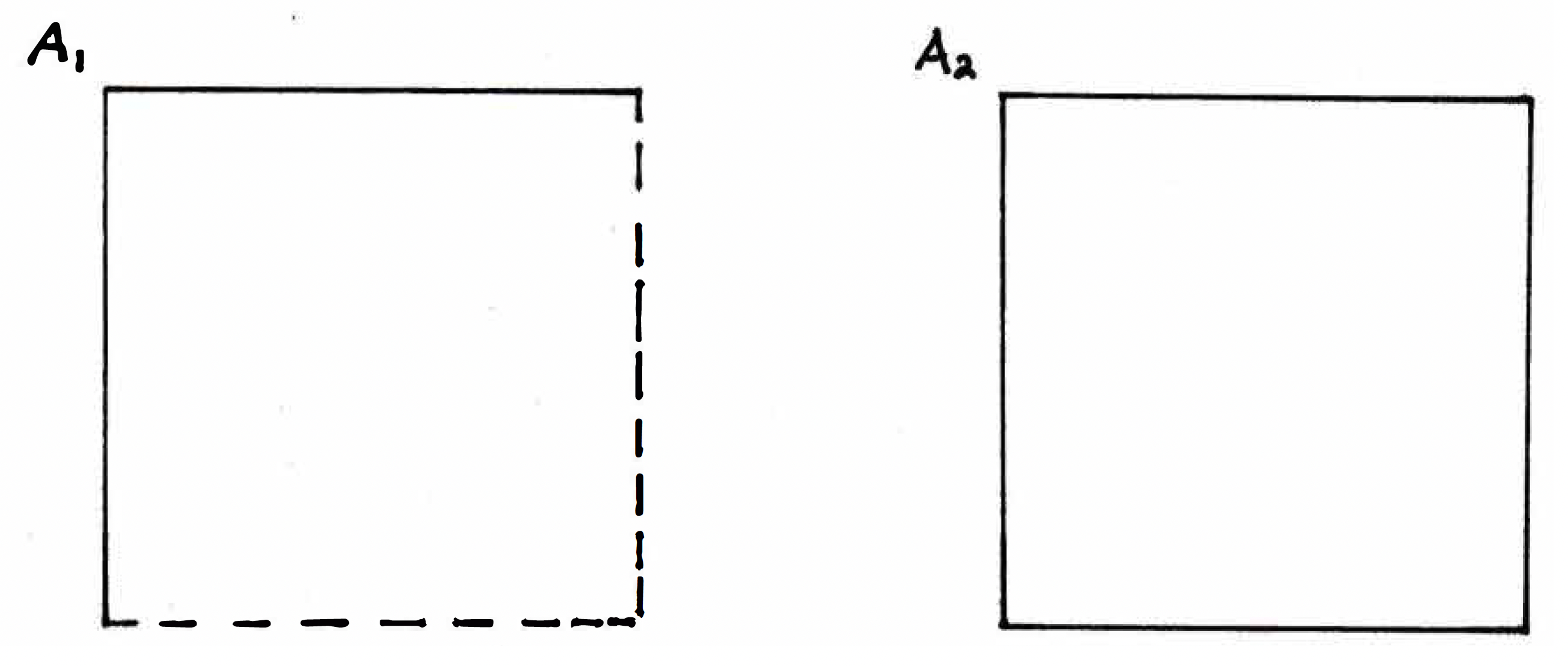
  Is the set $A_1$ open? No, not if it contains the pictured boundary points. Is $A_1$ closed? No, it does not contain all of its limit points. But if I throw in all of the limit points, which includes a lot of stuff but in particular the so-called boundary points, then I have what looks to be a closed set, namely $A_2$. In the context of closures and the set illustrations above, we have $\overline{A_1}=A_1\cup A_1'=A_2$. Is the set $A_2$, the closure of $A_1$, actually a closed set? We certainly hope so! We hope we gave it a good name. So let's try to prove that the closure of a set is, in fact, a closed set.

• The closure of a set is a closed set: To show $\overline{A}=A\cup A'$ is a closed set, we must show that $\overline{A}$ contains all of its limit points. But what is a limit point of $\overline{A}$? A point $p$ is a limit point of $\overline{A}$ if every neighborhood of $p$ contains a point $q\neq p$ such that $q\in\overline{A}$.\

  Suppose $p$ is a limit point of $\overline{A}$. We want to show that we must have $p\in\overline{A}$. If $p$ is a limit point of $\overline{A}$, then every neighborhood of $p$ contains a point $q\neq p$ such that $q\in\overline{A}$; that is, $q\in A$ or $q\in A'$.\

  If we take a limit point $p$ of $\overline{A}$, is it necessarily true that $p\in\overline{A}$? Every neighborhood of $p$ must contain a point $q\neq p$ in $\overline{A}$ but such a neighborhood seems to not necessarily contain a point of $A$.\

  To show $p\in\overline{A}$, we must show $p\in A$ or $p\in A'$; that is, the point $p$ is either in $A$ itself or $p$ is a limit point of $A$ (i.e., any neighborhood of $p$ contains a point of $A$). Consider any neighborhood of $p$, say $N_r(p)$. We want to show that $N_r(p)$ contains a point of $A$ if $N_r(p)$ is not already in $A$.\

  If $p\in A$, then we are done. Thus, assume $p\not\in A$. We will show that $N_r(p)$ contains a point of $A$. What do we know about $N_r(p)$? Since $p$ is a limit point of $\overline{A}$, we know $N_r(p)$ must contain a point of $\overline{A}$; let's call such a point $q$. Since $q\in\overline{A}$, it must be the case that $q\in A$ or $q\in A'$. If $q\in A$, then we are done. Thus, assume $q\not\in A$; that is, assume $q\in A'$. Then $q$ is a limit point of $A$; that is, $N_{r'}(q)$ contains a point of $A$; let's call such a point $q'$. Choose $N_{r'}(q)$ such that $N_{r'}(q)\subset N_r(p)$. If we can choose $N_{r'}(q)$ in such a way, then we will be done because we will have shown that any neighborhood of $p$, namely $N_r(p)$, contains a point of $A$, namely $q'\in N_{r'}(q)$. But how do we know a neighborhood $N_{r'}(q)$ such that $N_{r'}(q)\subset N_r(p)$ actually exists?\

  Since every neighborhood is an open set, it follows that $N_r(p)$ is an open set; that is, every point of $N_r(p)$ is an interior point of $N_r(p)$. Let $q$ be such an interior point. Then, by the definition of an interior point, there is a neighborhood $N_{r'}(q)$ such that $N_{r'}(q)\subset N_r(p)$. This concludes the proof.

• Every neighborhood is an open set: Why are neighborhoods open? Consider the following figure:

  

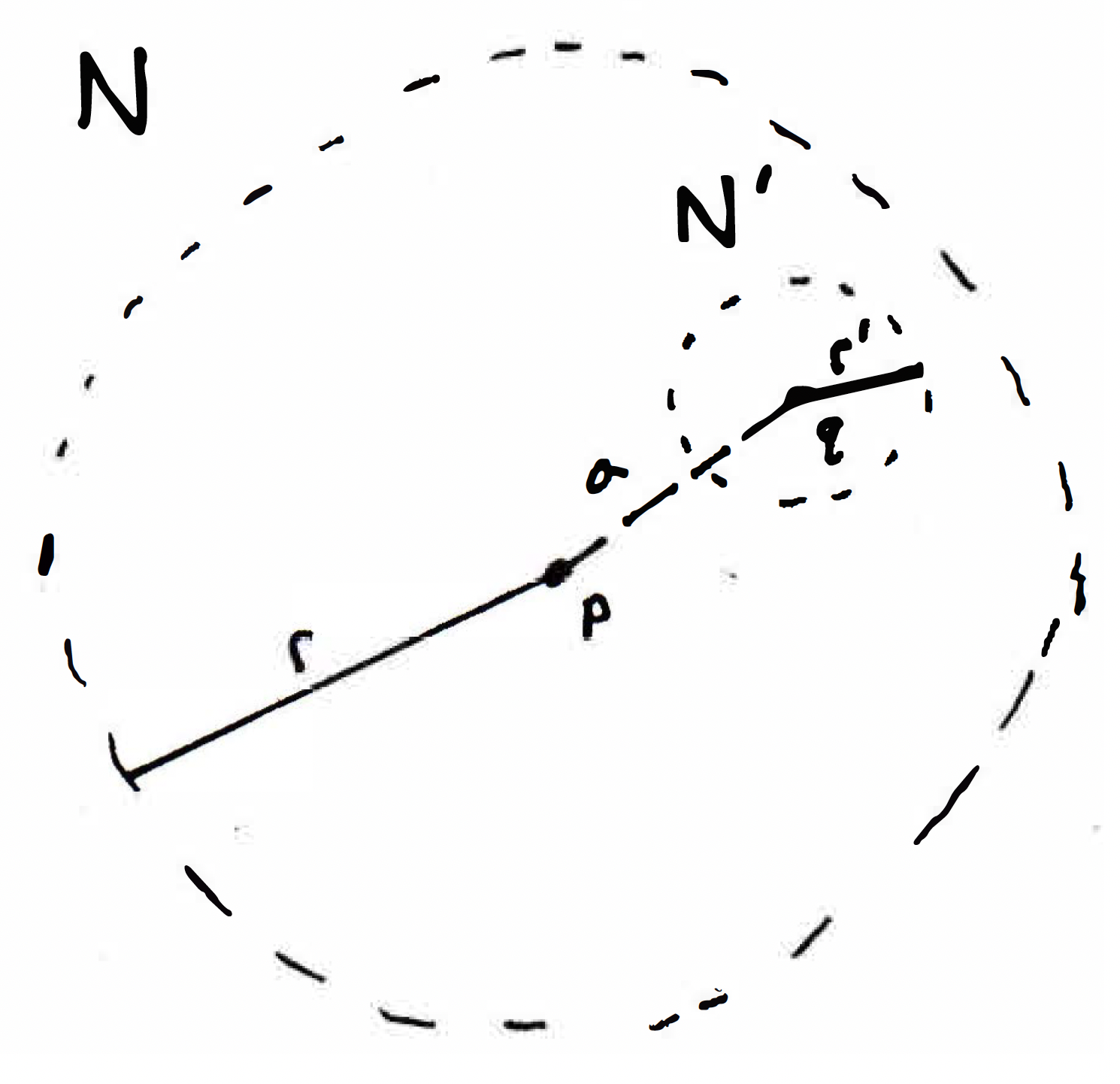
  Why is it that if you give me a point $p$ and a neighborhood around it, $N$, that I can find around any other point $q$ a neighborhood around it, $N'$, such that $N'\subset N$? The neighborhood of $p$ is defined by its radius. We can write the neighborhood of $p$ as $N_r(p)$ to communicate that $r$ is the defining radius of the neighborhood. What can we say about the distance from $p$ to $q$ in the picture above? We must have that $d(p,q)<r$. Let's call this $a$; that is, $a=d(p,q)<r$. What's the radius you would suggest that might work here to ensure that the neighborhood of $q$ is completely contained in the neighborhood of $p$? It seems like $r-a$ should work. Is $r-a$ positive? Yes, because $a=d(p,q)<r$. Let this suggested radius be denoted by $r'$; that is, $r'=r-a$. Our claim, then, is that anything that's distance less than $r'$ from $q$ is going to be distance less than $r$ from $p$. Why is that true? Triangle inequality! So this is really where we're using the metric. It's really important that we're in a metric space; otherwise, this neighborhood wouldn't necessarily be open. (It's important that we have the triangle inequality in order for neighborhoods to be open.) Our claim, more precisely stated, is that $N_{r'}(q)\subset N_r(p)$, and we can check this by noting that if the distance from some point $x$ to $q$ is less than $r'$, i.e. $d(x,q)<r'$, then $d(x,p)\leq d(x,q)+d(q,p)<r'+a=r$, the key observation being that $d(x,p)<r$, thus justify the claim that $N_{r'}(q)\subset N_r(p)$. The lesson here is that the triangle inequality is very important for this seemingly intuitive property to be true.

• A set is closed if and only if it is equal to its closure:

  • $(\rightarrow)$: If $E$ is closed then $E'\subset E$ so $E\cup E'\subset E$, and that means $\overline{E}\subset E$, and we clearly have $E\subset\overline{E}$. So $E=\overline{E}$.
  • $(\leftarrow)$: If $E=\overline{E}$, then $E$ contains all of its limit points; that is, $E$ is closed.

• If a set is a subset of another closed set, then the closure of such a set is also contained in the set: Let $F$ be a closed set. If $E\subset F$, then $\overline{E}\subset F$. What this is saying is, in some sense, we know $\overline{E}$ is a closed set and any other closed set that contains $E$ must contain $\overline{E}$. So, in some sense, the closure of a set, $\overline{E}$, is the smallest set that contains $E$. The moral of the story here is that $\overline{E}$ is the smallest closed set containing $E$.

  The proof sketch here is not too bad. If $F$ is a closed set, then $F$ contains all of its limit points. In particular, $F$ contains the limit points of $E$. Another way of communicating this is to say that if $p$ is a limit point of $E$, then $p$ is a limit point of $F$. But $F$ contains all of its limit points. So all of the limit points of $E$ are in $F$ as well. So $F$ contains the limit points of $E$ as well as $E$ itself. Thus, $\overline{E}\subset F$.

Relationship between open and closed sets

What is the relationship between open and closed sets?

• Motivation: We have this curious definition for an open set (i.e., a set $E$ is an open set if every point of $E$ is an interior point of $E$) and a curious definition for a closed set (i.e., a set $E$ is a closed set if every limit point of $E$ is a point of $E$), but they don't really seem all that related, and yet I claim there is an intimate relationship between open sets and closed sets. So what is the relationship?

• Relationship between open and closed sets: In a metric space $X$, we claim that $E$ is open if and only if $E^c$ is closed, where $E^c$ stands for the complement of $E$ and is defined as the set of all points not in $E$; that is, $E^c$ contains all of the points in $X$ but not in $E$ or simply $E^c=X\setminus E$. Or differently, $E=\{p\in X \mid p\not\in E\}$. Is it true that if I am outside of a closed set then I can take a point and push it around a little and still be outside of that closed set? Yes. So let's see if we can justify this fact. Why is this theorem true?

  Let $E$ be an open set. Then any point $x\in E$ is an interior point. What that means is that for any $x\in E$ there exists a neighborhood $N$ of $x$ such that it is contained entirely in $E$ or, equivalently, that $N$ is disjoint from $E^c$. So we just turned this into a statement about the complement of $E$. Consider the picture below.

  

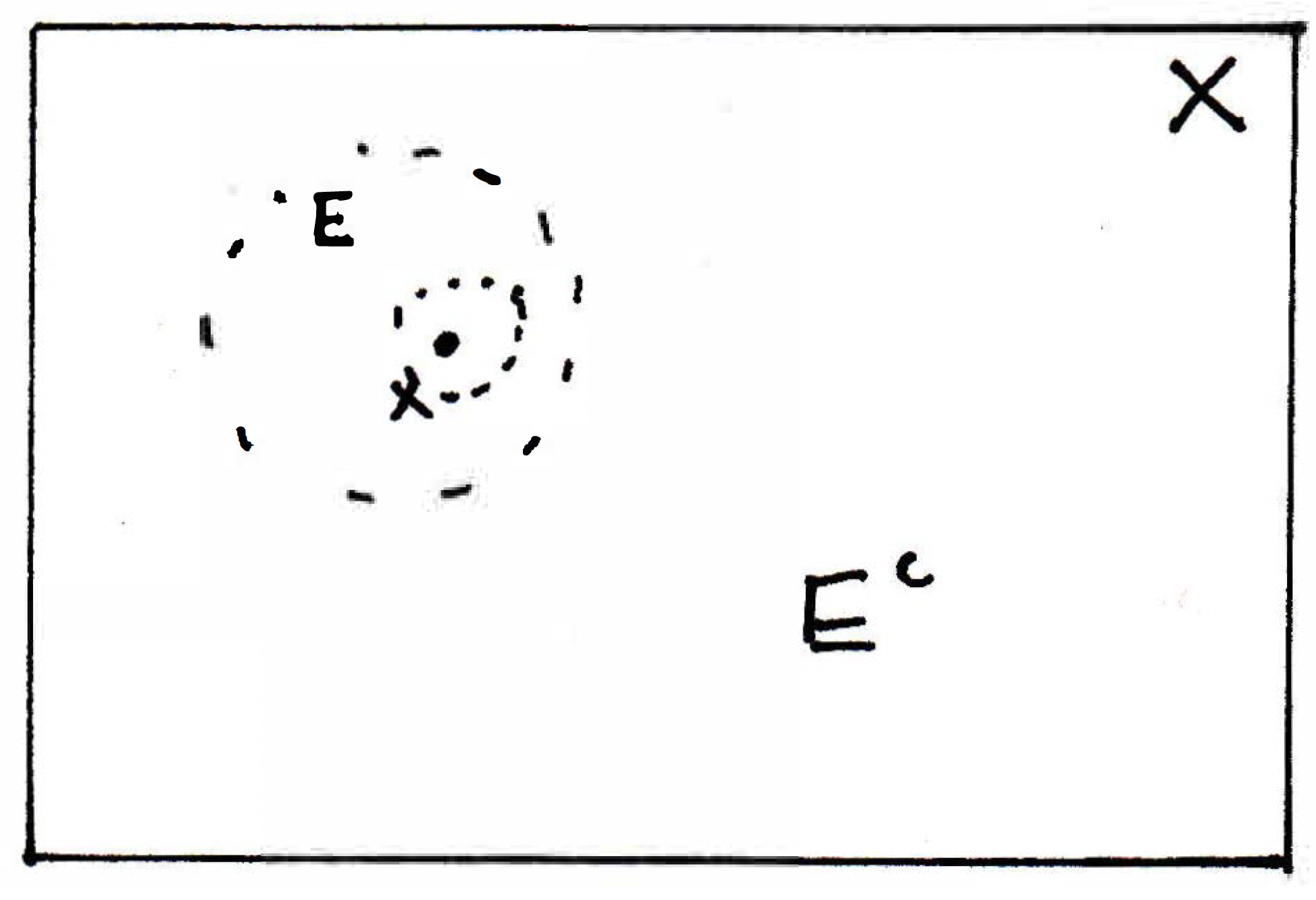
  We have an open set $E$ and an arbitrary point $x\in E$, and the claim is that if $x$ has a neighborhood around it that is completely within $E$, then the neighborhood of $E$ completely misses $E^c$ which sits outside of $E$ but in the metric space $X$. What's the goal here? The goal is to show that $E^c$ contains all its limit points. And I've just picked an arbitrary point $x$ that's not in $E^c$ that has a neighborhood that completely separates it from $E^c$. So could this point $x$ be a limit point of $E^c$? No! Therefore, $E^c$ contains all of its limit points. More precisely, for any $x\in E$, $x$ is not a limit point of $E^c$. (This is because if $x$ were a limit point of $E^c$ then any neighborhood of $x$ should contain a point of $E^c$, but the one we've chosen does not (as pictured above). Hence, $E^c$ contains all of its limit points. We could display the outline of the proof as follows to illustrate the if and only if nature holds:

  $$\begin{align*} \text{$E$ is open} &\iff \text{any point $x\in E$ is an interior point of $E$}\\[1em] &\iff \text{for every $x\in E$, there exists a neighborhood of $x$ such that $N$ is disjoint from $E^c$}\\[1em] &\iff \text{for every $x\in E$, $x$ is not a limit point of $E$}\\[1em] &\iff \text{$E^c$ contains all its limit points}.\\[1em] &\iff \text{$E$ is closed}. \end{align*}$$

  So complements of open sets are closed and complements of closed sets are open. What can we say about unions of open sets? As an aside, are the rationals a closed set? No, because it does not contain all of its limit points. We can approach $\sqrt{2}$ using rational points. So it's not closed. Are the rationals an open set? If I perturb a rational will it necessarily remain rational? No, or if you like, around any rational can I find an open set consisting of only rationals? No. So the rationals are neither open nor closed.

• Unions of open sets: Is the union of two open sets open? Yes. Why? Every point of a union of two open sets was interior to one of the sets so it's true then, in the union of the two sets, that every point will be interior to their union because such a point has a neighborhood around it completely contained in one of those two sets, so therefore contained in both of those sets. Okay, what if I take a union of infinitely many open sets? Is that still open? What about closed sets? If I take the union of two closed sets, is the union closed? Yes, we should be able to come up with an argument for that, but it seems likely. What about the union of infinitely many closed sets? Is that necessarily closed? No, we may have some examples ready to give.

• Unions and intersections: Suppose we look at the following sets $K_i=[-1+\frac{1}{i},1-\frac{1}{i}]$, which are closed sets centered around 0. If we union everything, then we get $\bigcup_{i=1}^\infty K_i=(-1,1)$, which is not closed. Suppose $\{E_\alpha\}$ is a collection of sets (where we use $\alpha$ here to make it clear that there may be uncountably many sets in our collection; $\alpha$ is just an element of some indexing set $A$, where $A$ may be uncountable; one is typically used to using an indexing set of natural numbers, but the indexing set could also be the set of real numbers). Then

  $$\biggl(\bigcup_{\alpha\in A} E_\alpha^c\biggr)^c=\bigcap_{\alpha\in A} E_\alpha^c.$$

  Let's prove this. We have the following:

  $$\begin{align*} x\in\biggl(\bigcup_{\alpha\in A} E_\alpha^c\biggr)^c &\iff x\not\in E_\alpha\ (\text{for any $E_\alpha$})\\[1em] &\iff x\in E_\alpha^c\ (\text{for all $\alpha$})\\[1em] &\iff x\in\bigcap_{\alpha\in A} E_\alpha^c. \end{align*}$$

  This fact will be very useful to us now that we have noted that open sets are complements of closed sets.

• A four-part theorem: We have the following:

  • An arbitrary union of open sets is, in fact, open.
    • Proof. If $x\in\bigcup_\alpha U_\alpha$, where each $U_\alpha$ is open, then what does it mean for $x$ to be in the union $\bigcup_\alpha U_\alpha$? Well, that means $x$ is in at least one of the sets $U_\alpha$. Our goal here is to show that every point $x$ in the union $\bigcup_\alpha U_\alpha$ has a neighborhood around it that's completely contained inside $\bigcup_\alpha U_\alpha$. Okay, since $x\in\bigcup_\alpha U_\alpha$, it must be the case that $x\in U_\alpha$ for some $U_\alpha$. So $x$ has a neighborhood $N_x$ such that $x\in N_x\subset U_\alpha$, but $U_\alpha\subset \bigcup_\alpha U_\alpha$, as desired. So we have the desired neighborhood.
    • The arbitrary intersection of closed sets is closed.

    • Proof. Suppose $B_\alpha$ are closed. Then $U_\alpha=B_\alpha^c$ are open. So these are a bunch of things that are open and the union of a bunch of open sets is open. So its complement is closed. But isn't $U_\alpha^c$ just $B_\alpha$? Recall we established that

      $$\biggl(\bigcup_{\alpha\in A} E_\alpha^c\biggr)^c=\bigcap_{\alpha\in A} E_\alpha^c.$$

      What we have here is that

      $$\bigcap_{\alpha\in A} U_\alpha^c=\biggl(\bigcup_{\alpha\in A} B_\alpha^c\biggr)^c \qquad\text{or simply}\qquad \bigcap_{\alpha\in A} B_\alpha=\biggl(\bigcup_{\alpha\in A} U_\alpha\biggr)^c;$$

      that is, the arbitrary intersection of closed sets $B_\alpha$ is the complement of an arbitrary union of open sets $U_\alpha$. From above, we know that an arbitrary union of open sets is open, and we also know that the complement of an open set is closed. Thus, the arbitrary intersection of closed sets $B_\alpha$ is closed, as desired.

    • The intersection of a finite collection of open sets is open, whereas the arbitrary intersection of open sets is not open; for example, consider $\bigcup_{i=1}^\infty(-\frac{1}{n},\frac{1}{n})=\{0\}$, which is closed.

    • Proof. To establish this, you have to do something slightly different. If I intersect to two open sets $U_1$ and $U_2$, then why is their intersection going to be open? Why is it that if I pick a point in the intersection then it will be an interior point of the intersection? Consider the picture below:

      

      Why is it that $U_1\cap U_2$ will be open? Why is it that if I pick a point in their intersection then this point will be an interior point of the intersection? We know this point in the intersection is an interior point of $U_1$ and also an interior point of $U_2$, so why is it an interior point of both of them (i.e., the intersection)? Consider the point pictured in the figure with two concentric dashed circles around it. The smaller concentric circle represents the interior point contained entirely in $U_1$ while the larger concentric circle represents the interior point contained entirely in $U_2$. How do I know this point, which is certainly in the intersection of $U_1$ and $U_2$ is actually an interior point of $U_1\cap U_2$? Take the interior point with a neighborhood of smaller radius! In the picture above, this means taking the interior point contained entirely in $U_1$. So for finitely many open sets you would do what? Take the minimum radius one. Now, why would this idea fail in the case of infinitely many intersections? What would go wrong with this idea? The minimum would not necessarily exist because the concentric circles could get smaller and smaller and smaller. So it doesn't have a minimum. It has an infimum, but it's not going to be greater than 0. That's the problem. So here's the sketch. There exists a neighborhood $N_{r_i}(x)$ for each $U_i$. Let $r=\min(r_1,\ldots,r_n)$. Then $N_r(x)$ shows $x$ is interior to $\bigcap_{i=1}^n U_i$.

    • The union of a finite collection of closed sets is closed.
    • Proof. This follows from above (by taking complements) in a similar way that the second proof follows from the first.

Other definitions

What are some other definitions that might be useful before calling it a day?

• Density of a set in a metric space: A set $E$ is said to be dense in a metric space $X$ if every point of $X$ is a limit point of $E$ or in $E$ (or both). So an example of this would be that $\Q$ is dense in $\R$ because isn't it true that every point in $\R$ is a limit point of $\Q$ or a rational number itself? That is true. Here's another way of saying this: If every point of $X$ is a limit point of $E$ or in $E$, then every point of $X$ is necessarily in the $\overline{E}$, the closure of $E$. So we could say that $E$ is dense in $X$ if $\overline{E}=X$. Or, alternatively, if we have that $\overline{E}=X$, then that means that any open set in $X$ contains a point in $E$ — that's what $\overline{E}=X$ means. You give me any point in $X$, then any open set around it contains a point of $E$. In sum, the following are all equivalent ways of saying that a set $E$ is dense in $X$:

  1. A set $E$ is said to be dense in a metric space $X$ if every point of $X$ is a limit point of $E$ or in $E$ (or both).
  2. $\overline{E}=X$.
  3. Any open set of $X$ contains a point in $E$.

  To give some intuition as to what this might mean for other metric spaces, you might want to know, for example, if I have a bunch of functions, can I approximate it by sines and cosines, or sums of sines and cosines. That's what Fourier analysis is all about. That is, in some sense, asking the question of whether or not a certain subset of functions is dense in a whole space of functions. Is the set of all polynomial functions dense in the set of all continuous functions? Is the set of linear combinations of sines and cosines dense in a set of periodic functions? That's really what we're saying.