3 - Construction of R

Where we left off last time

We discussed our construction of the rational numbers

$$\Q=\{\tfrac{p}{q}, q\neq0\}$$

where $\frac{p}{q}$ is the class of ordered pairs $(p,q)$ under the usual equivalence relation for fractions. Of course, we think of rational numbers as fractions, and fractions are, in fact, ordered pairs of integers. You have a number on top and a number on the bottom. And the way we thought about this was these ordered pairs satisfied some notion of equivalence, and it's just the usual notion of equivalence that you are used to, that you were taught in grade school for how to tell whether or not two fractions actually represented the same thing.

What we've seen is, in fact, this is an equivalence relation. We've seen that under this definition we can actually construct an addition and a multiplication that's well-defined. So it gives this collection of ordered pairs a structure, an arithmetic structure. (That is, $\Q$ has well-defined operations $+$, $\times$, an order, and "contains" $\Z$.) And it has an order, which, if you recall, an order relation satisfies two properties:

1. Trichotomy: Whatever the relation is, say, "less than" or "$<$", then if you take two elements, say $x$ and $y$, then you have exactly one of the following things:

   1. $x<y$ or
   2. $y<x$ or
   3. $x=y$

2. Transitivity: If $x<y$, and $y<z$, then $x<z$.

If trichotomy and transitivity hold for a set $S$, then we say $S$ has an order relation. From last time, we know that $\Q$ has a nice order relation that we defined. Despite the sophistication, the essential message is that it is all what you learned in grade school. From now on out, since we've carefully constructed the rationals, we can think of rationals as fractions. And $\Q$ contains $\Z$ in a very natural way.

Recall: why is Q nice?

• We also saw that $\Q$, in fact, is nice, because not only does it have these arithmetic operations, but it has the ability to solve certain equations that we couldn't solve in the integers before. For instance, $3x=5$ can't be solved in $\Z$ for $x$. But it can be solved in $\Q$ because $\Q$ is a field and it satisfies certain addition properties A1--A5, multiplication properties M1--M5, and distribution (which basically says addition and multiplication have to play nicely with each other) of multiplication over addition.

• We saw that not only do the rationals have an order and are a field but that they are an ordered field. This means that $\Q$, in addition to being ordered and being a field, that the order and the field properties play nice with each other. In particular, if I look at two rational numbers and I add the same thing to them, then their order relation should stay the same. Or if I multiply them by a positive rational number, then they should still preserve the same order.

• We finished last time by noting that $\Q$ is not large enough to solve all equations. In particular, $\Q$ is not large enough to contain solutions to the equation $x^2=2$, an equation whose solution has a very natural geometric interpretation:

  

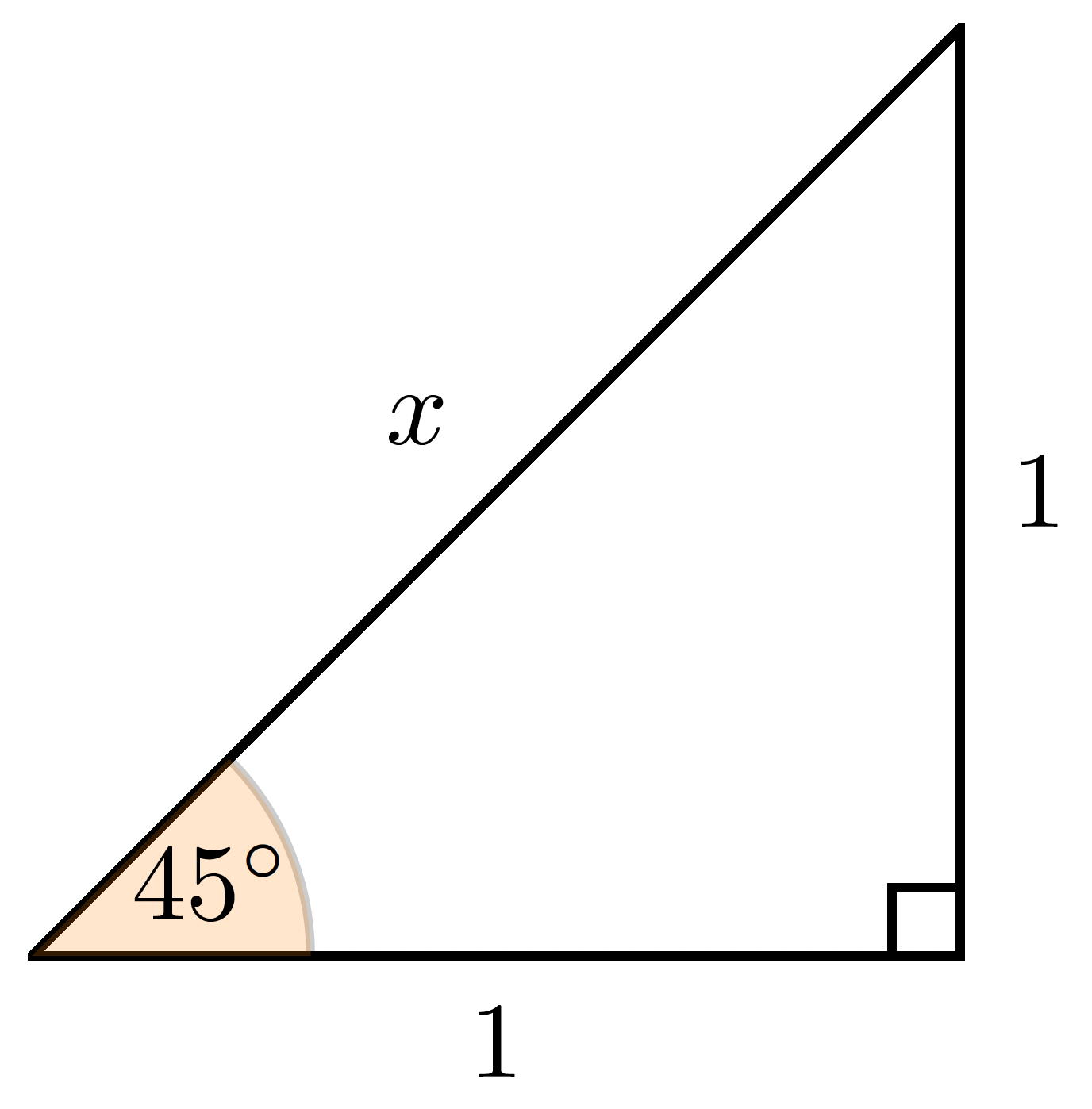
  As we can see from the above, by the Pythagorean Theorem, the hypotenuse has a length that solves the equation $x^2=2$, but this solution is not contained in $\Q$ (last time we showed that $x^2=2$ does not have a solution in $\Q$).

• Our plan is to rectify that problem above by looking for a construction that would allow us to solve equations like $x^2=2$. We will do so by "Dedekind cuts" which were introduced by Richard Dedekind in 1872. What do we mean by "construct" the real numbers? The situation will be very much like what we did for the rationals. The idea you should have in your head is that if you have a number line, because we have an order, we can place the rationals along such a number line. We can mark off the integers and rationals. The idea is that there are some holes, in some sense, on the number line. If the Pythagorean length $\sqrt{2}$ (i.e., what we are calling the square root of 2 even though we haven't actually defined what we mean by square root), if we look at the hypotenuse of a right triangle with sides 1 and 1, as above, then the length of that hypotenuse is somewhere on the number line, and yet there is not a rational that spans that length. In this sense, there are some holes on the real line.

• We want a construction of the reals, but what do we mean, again, by "construct" the reals? What we mean is we want a construction that only depends on things we've already defined. Just like the rationals, we defined those in terms of integers, as ordered pairs of integers. But we did this in a fashion that only depended on things we did before.

• If I want to define the real numbers, I can't say "let's fill this in" because that would not have any meaning. What does it mean to fill in the number line? I don't even know where the holes are. So how will I get at the fact that I have some gaps here without talking about the gaps?

• Since $x^2=2$ does not have a solution in $\Q$, it might be worthwhile, then, to look at the other possibilities, namely that $x^2>2$ or $x^2<2$ (by trichotomy, these are the only other possibilities). Consider the set $A=\{x\in\Q \mid x^2<2\}$, which is the set of all rationals $x$ whose square is less than 2. What does that set look like on the number line? It's a set consisting of all the rationals roughly between $-1.42$ and $1.42$. If we look at the set $A$ in more detail, then it has an interesting problem. What's the problem? The problem is there is nothing at the very edge. We wish that there was, but there isn't. This points to a property that we want to get at. We'll give it a name, and we'll explore what it means for our construction. It points to the idea of what is called a least upper bound. What do we mean by that? If you take a look at the number line, the fact that there is not a number right at the very end is related to the idea that there are a bunch of points to the right that are greater than any of the numbers in the set $A$. We would call, for instance, 2.2 an upper bound of $A$. So 3.1 is also an upper bound of $A$. We know 1.5 is also an upper bound even though we will concretely show it in a moment. The idea we are trying to get at is whether or not there is a least upper bound, and the problem in $\Q$ is that there may not be a least upper bound.

What is the deal with least upper bounds?

• Upper bound (definition): Suppose $S$ is an ordered set, and $E\subset S$. If there exists a $\beta\in S$ such that $x\leq\beta$ for every $x\in E$, we say that $E$ is bounded above, and call $\beta$ an upper bound of $E$. (Lower bounds are defined in the same way with $\geq$ in place of $\leq$.)

• Examples: It may help to look at a few examples where upper bounds are involved.

  1. We mentioned before that 2 was an upper bound for $A$. This seemed pretty obvious. Less obvious, perhaps, was whether or not $\frac{3}{2}$ was an upper bound for $A$. So let's look at that. If $\frac{3}{2}$ is not an upper bound, then there exists $x\in A$ where $x>\frac{3}{2}$ and $x^2>\bigl(\frac{3}{2}\bigr)^2>2$. But this implies $x\not\in A$, a contradiction.

• Least upper bound (definition): Suppose $S$ is an ordered set, $E\subset S$, and $E$ is bounded above. Suppose there exists an $\alpha\in S$ with the following properties:

  1. $\alpha$ is an upper bound of $E$

  2. If $\gamma<\alpha$ then $\gamma$ is not an upper bound of $E$.

     Then $\alpha$ is called the least upper bound of $E$ (that there is at most one such $\alpha$ is clear from (ii)) or the supremum of $E$, and we write

     $$\alpha=\sup E.$$

• The word supremum kind of suggests that "to be supreme" means to be bigger than everything, but it's the least biggest thing. It's sort of what might be at the endpoint discussed earlier if there were anything there.

• Properties of suprema: Which sets have suprema? Here are some examples (throughout the examples, let $S=\Q$).

  1. Let $E=\{\frac{1}{2},1,2\}$. What is the supremum? We see that $\sup E=2$. To see this more clearly, suppose there were an upper bound less than 2, call it $\gamma$, then $\gamma$ would not be bigger than 2. And therefore $\gamma$ would not be an upper bound for $E$. This is just one example, but we could throw some more numbers into the mix. If we added the number 1.5 to $E$, then $\sup E=2$ yet again. If we added 15 to $E$, then $\sup E=15$. We could keep throwing in numbers, but can we generalize a statement about a finite collection of objects? Yes, it's the last number on the number line for the collection. Ultimately, we can say that a finite set has a supremum.

  2. Let $E=Q_{-}$ or the negative rationals. Does this have a supremum? Yes, $\sup E=0$. How do we know this? How do we know that there isn't some incredibly small number that's just to the left of 0 that's greater than all the negative rationals? Because given any negative rational $\gamma$, we can find a negative rational $\eta$ where $\gamma<\eta$. In particular, we could take $\eta=\frac{\gamma}{2}$ to illustrate our point (i.e., $\frac{\gamma}{2}$ would be closer to 0 from the left than $\gamma$ would be). So $\gamma$ would not be an upper bound. We can apply this thought process to any given negative rational $\gamma$, definitely making $\gamma$ not an upper bound. This is an example of an infinite set, namely $\Q_{-}$, that does have a supremum.

  3. Let $E=\Q$. Does $\sup E$ exist? Not in the conventional sense at least. The reason $\Q$ does not have a supremum is not that it failed property (ii) above but because it failed property (i). That is, there is not an upper bound at all for $\Q$. The set $\Q$ is unbounded above. In the extended real number system, we communicate this by writing $\sup\Q=+\infty$. This is very different from the situation concerning $A=\{x\in\Q\mid x^2<2\}$.

  4. Let $E=A$, where $A=\{x\in\Q\mid x^2<2\}$. What is $\sup A$? Does $A$ have a least upper bound in $\Q$ (which is all we have right now)? We see that $\sup A$ does not exist, but how do we prove that? It is not because $A$ is unbounded, as was the case with $\Q$ above. It does not exist even though $A$ is bounded. We noted earlier that $A$ is bounded above by $\frac{3}{2}$, for instance. Thus, this is a more essential kind of failure to not have a supremum than was the case with $\Q$.

  5. To prove that $\sup A$ does not exist, see [17]. Nonetheless, let's suppose we have an upper bound for $A$ in $\Q$. One way to show that $\Q$ doesn't have a least upper bound for $A$ is to show that, no matter what upper bound you give me, I can always find a smaller one. Let's suppose we are given an upper bound, say $p$. Can we devise a way to come up with a number that is between the rightmost edge of $A$ and our choice of $p$? In the example involving $E=\Q_{-}$, we considered a negative rational $\gamma$, but we showed $\gamma$ could not be an upper bound by considering $\frac{\gamma}{2}$. There's a temptation in this case involving the set $A$ to average $p$ with $\sqrt{2}$ or the square root of 2, but we don't have a square root of 2 (yet). Because we can't do that, we have to be a bit more clever. Instead of associating with each number $q$ the number $\frac{p+\sqrt{2}}{2}$, which would be a cheat since we don't have a notion of $\sqrt{2}$ just yet, Rudin suggests associating with each number $q$ a number slightly less than $p$ (which thankfully only involves $p$), namely,

  $$q=p-\frac{p^2-2}{p+2}=\frac{2p+2}{p+2},$$

  and it's enough to get you what you want; that is, it produces a $q$ that is somewhere between the rightmost edge of $A$ and our originally chosen $p$.

• Motivation for $\R$: We have this notion now of a least upper bound, the supremum, and whatever we do to construct the reals, the reals (unlike the rationals) will not have bounded sets that do not have suprema. That's the surprising thing. We'll construct $\R$ only involving rationals in such a way that it'll be obvious that $\R$ has what is called "the least upper bound property." We will construct $\R$ and prove the main theorem in Chapter 1 from Rudin.

How do we construct R?

• Theorem: There exists an ordered field $\R$ which has the least-upper-bound property. Moreover, $\R$ contains $\Q$ as a subfield. [This is the core theorem of Chapter 1 in Rudin.]

• Structure of our proof: There are three things we are going to show.

  1. Ordered field: The set $\R$ is an ordered field.
  2. Least-upper-bound property: The set $\R$ has the least-upper-bound property.
  3. Containment: The set $\R$ contains $\Q$ as a subfield.

• Least upper bound property (definition): It basically says if the supremum of a set does not exist, then it must be the case that the set is unbounded. It will not be the case that bounded sets lack suprema. The more formal statement of the definition is given below.

  Definition. An ordered set $S$ is said to have the least-upper-bound property if the following is true: If $E\subset S$, $E$ is not empty, and $E$ is bounded above, then $\sup E$ exists in $S$.

  Such a set $S$, as mentioned in the definition above, is often said to have the "lub" property or that it satisfies the so-called completeness axiom.

• The empty set: What happens if $E=\emptyset$? Is 2 an upper bound for $E$? Does 2 have the property that for element $\gamma$ in the empty set that $\gamma<2$? Yes. So everything is an upper bound for the empty set. Why is this true? It's vacuously true! There's nothing in the empty set.

How do we construct R from Q?

• The task ahead: Remember our task is to construct the real numbers in a way that only involves things we've defined before, namely the rationals. How is it that we are going to get at the idea that there ought to be something right on the far-right edge of $A$, right on the cutting edge. How are we going to get at that idea? The idea of Dedekind was to think about the real numbers as just being some collection of rationals. Just like we thought of the rationals as an ordered pair of integers, we'll think of the real numbers as collections of rational numbers that are specified, in some sense, by a cut. We are going to make a cut at the rightmost edge of $A$ and say that everything to the left of this cutting location is a collection of rationals and that this collection is a cut.

• Cut (definition): A cut $\alpha$ is a subset of $\Q$ such that the following conditions hold:

  1. $\alpha$ is not empty, and $\alpha\neq\Q$\hfill[the cut is said to be nontrivial in this case]

  Note A cut is nontrivial. That is, a cut is neither empty nor everything — we want $\alpha$ to be some thing but not all things.

  2. If $p\in\alpha$, $q\in\Q$, and $q<p$, then $q\in\alpha$

  Note A cut is closed downward. A cut will be a collection that is, in some sense, closed downwards. What is meant by that is if you take some cut member, say $p\in\alpha$, and then you have a rational $q$ (i.e., $q\in\Q$) that is less than $p$ (i.e., $q<p$), then this rational $q$ must also be a member of the same cut as $p$ (i.e., $q\in\alpha$). In this sense, the condition above means a cut is "closed downward" or "closed to the left."

  3. If $p\in\alpha$, then $p<r$ for some $r\in\alpha$.

  Note A cut is unbounded above. In some sense, a cut is like the picture of the set $A$ in the sense that it does not have a biggest member. No largest member. In other words, there's something to the right of $p$, namely $r$, that is also a member of the cut $\alpha$.

  A set $\alpha\subset\Q$ that fulfills criteria (i)-(iii) listed above is called a Dedekind cut.

• Informal thoughts about cuts: Essentially, a cut should be thought of as the set of all rational numbers to the left of some point in the real line. Since we have not constructed the real line yet, we cannot define a cut in that simple way; we have to make the construction more indirect. Nonetheless, given the properties of a cut above, these properties essentially describe a set that looks like a "rational halfline" (in the sense that our cut represents the half of the rationals to the left of wherever the cut is made). If $\alpha$ is a cut and $p\not\in\alpha$, then any rational $q>p$ is also not in $\alpha$. Also, if $q\in\alpha$ and $p\not\in\alpha$, then it must be the case that $p>q$. (See [13] for more on this paraphrasing.)

• Examples of cuts: Let's consider some examples involving the idea of cuts.

  1. Is the set $A$, which we defined before as $A=\{x\in\Q\mid x^2<2\}$, a cut? No. Which property does it not satisfy? Let's see.

     • Property (i): Yes. The set $\alpha=A=\{x\in\Q\mid x^2<2\}$ is clearly nontrivial since $\alpha\neq\emptyset$ and $\alpha\neq\Q$.

     • Property (ii): No. This is where we run into an issue. Choose any rational lower bound $q$ for $A$. Then for some $p\in A$ and our $q\in\Q$, we have $q<p$, but $q\not\in A$. For example, if $q=-\frac{3}{2}$, then $q<p$, but $q^2=\frac{9}{4}>2$, and hence $q\not\in A$.

     • Property (iii): Yes. The set $A$ has no largest member. Recall this was one of the goals in establishing our choice of $q=p-\frac{p^2-2}{p+2}=\frac{2p+2}{p+2}$ from before. In [17], we consider some rational $p$ in $A$ and associate with it some rational $q$ slightly smaller than $p$, and end up showing that $q$ is in $A$. In the language of cuts, specifically the statement of condition (iii), we have the following:

       $$\text{If $p\in A$, then $p<q$ for some $q\in A$.}$$

       In Rudin's exposition, this $q$ is $q=\frac{2p+2}{p+2}$.

  2. Is the set $\alpha=\Q_{-}$, the set of all negative rationals, a cut? We must check the three given properties.

     • Property (i): Yes. The set $\alpha=\Q_{-}$ is clearly nontrivial since $\alpha\neq\emptyset$ and $\alpha\neq\Q$.
     • Property (ii): Yes. The set $\alpha$ is clearly closed downward because a rational number that is more negative than another negative rational number is still a negative rational number.
     • Property (iii): Yes. Given a negative rational number $\gamma$, there certainly exists another negative rational number $\eta$ that is greater than our given rational number. Using our work from before, we can consider $\gamma\in\alpha$. Then $\gamma<\eta$ for some $\eta\in\alpha$, namely $\eta=\frac{\gamma}{2}$.

     Since $\Q_{-}$ satisfies conditions (i)-(iii) for cuts, we know that $\Q_{-}$ is, indeed, a cut.

  3. Is the set $\beta=\{r\in\Q\mid r\leq 2\}$ a cut?

     • Property (i): Yes. The set $\beta$ is clearly neither nonempty nor equivalent to $\Q$.
     • Property (ii): Yes. Given some rational $p$ less than or equal to 2 and another rational $q$ less than or equal to 2 and also less than $p$, then it will clearly be the case that $q$ is also a rational less than or equal to 2.
     • Property (iii): No. For example, if $p=2$, then $p\in\beta$, but it is not the case that $p<r$ for some $r\in\beta$ since $p$ in this case is an upper bound for $\beta$.

  We are starting to get some idea as to what cuts ought to do just by their properties, but it's still unclear exactly what kinds of things or sets could be cuts. Instead of looking at more particular examples of cuts, we will simply look at the set of all cuts, and we will declare such a collection to be the real numbers.

How do we construct R by looking at it as the set of all cuts?

• Defining $\R$ in terms of cuts: Let $\R=\{\alpha\mid\alpha\ \text{is a \textit{cut}}\}$. There, that is our definition of the real numbers. What!? That is a little strange. A little strange. But the point is once we prove properties about real numbers that we are comfortable with, then we'll just think about the reals as we normally do. But for now, what do you think the cut will be that corresponds to the square root of 2 or $\sqrt{2}$? Maybe we start with something a littler easier. What cut would correspond with the number 1? How about cutting the number line at 1 and looking at all of the rationals less than 1? What cut would correspond with the number 3? All the rationals to the left of 3. Good. What about the square root of 2 now? All the rationals that are, in some sense, to the left of the rightmost edge of $A$ so it might look like $A$ somewhat but it had better include all of the rationals to the left of the rightmost edge of $A$. That's kind of the idea. So let's see that this actually behaves the way we expect it does, and that's maybe the surprise.

• Overview: The set $\R$, defined in terms of Dedekind cuts, will satisfy all of the properties that we expect the real numbers to satisfy. In particular, $\R$ will be an ordered field with the least-upper-bound property, and it will contain $\Q$. So the first thing we should maybe do is define what the order is.

• Defining an order: The set $\R=\{\alpha\mid\alpha\ \text{is a \textit{cut}}\}$ is a structure, but what kind of structure is it? The set $\R$, we will show, has structure; in particular, it will have an order, an arithmetic, and the field operations. We will define an order as follows (note that $\alpha$ and $\beta$ below are collections of rationals):

  Definition. Define "$\alpha<\beta$ to mean the following: $\alpha$ is a proper subset of $\beta$. (Note that we do not mean $\alpha<\beta$ if $\alpha\subset\beta$ but iff since we are making a definition.) That is, $\alpha\subset\beta$ but $\alpha\neq\beta$.

  An aside: In terms of how we would make sense of the square root of 2 as $\R$ is currently defined, the point is that we will not have to refer to the square root of 2 in making our definition (because doing so would be meaningless). To hint at the idea, recall the set $A=\{x\in\Q\mid x^2<2\}$ that did not have a least upper bound in $\Q$; well, in $\R$, the set $A$ actually will have a least upper bound once we actually discuss how to take supremums involving $\R$ where we've defined $\R=\{\alpha\mid\alpha\ \text{is a \textit{cut}}\}$. For right now, you should check that "$<$" is an order. See [17] for such a demonstration. You should fill in this demonstration a bit. But very briefly:

  Trichotomy: Is it possible for $\alpha$ to be less than $\beta$ and for $\beta$ to be less than $\alpha$? No, given proper containment. That's clear. And the only way that they are equal is if there is equal containment. Does it satisfy transitivity? Clear. But you should check. It is an order.

• Operations: We want to know whether or not $\R$ has operations that we can deal with. This is the amazing thing — we can actually define an operation. How might we define addition for instance? Recall that $\alpha$ and $\beta$ are both collections of rational numbers. How might we define $\alpha+\beta$, a new collection of rational numbers?

• Addition (definition): If $\alpha\in\R$ and $\beta\in\R$, then define $\alpha+\beta$ to be the set of all sums $r+s$, where $r\in\alpha$ and $s\in\beta$. That is, $\alpha+\beta=\{r+s\mid r\in\alpha,s\in\beta\}$. It helps to note here, perhaps, that all of the elements of $\R$ are sets, namely a bunch (i.e., a collection) of cuts where each cut represents a set of rational numbers. The set $\alpha+\beta$ is a collection of rational numbers (the elements of $\alpha$ and $\beta$ are both rational numbers, and the set of rational numbers is closed with respect to addition), but is the set $\alpha+\beta$ a cut? We must check that $\alpha+\beta$ is, in fact, a cut.

  • Property (i): Yes. Is $\alpha+\beta$ nontrivial? If there is something in $\alpha$ and something in $\beta$, then is there not something in $\alpha+\beta$? Clearly there must be. And if $\alpha$ is not everything and $\beta$ is not everything, then is $\alpha+\beta$ not everything? We'd have to check. If $\alpha$ is not everything, then $\alpha$ has an upper bound, say $M$. If $\beta$ is not everything, $\beta$ has an upper bound, say $N$. Is there an upper bound for $\alpha+\beta$? Yes, we claim the upper bound is $M+N$. So $\alpha+\beta$ does not contain everything. For Rudin's description below, replace $r'$ with $M$ and $s'$ with $N$ to get Su's description.

    Rudin: It is clear that $\alpha+\beta$ is a nonempty subset of $\Q$. Take $r'\not\in\alpha$, $s'\not\in\beta$. Then $r+s<r'+s'$ for all choices of $r\in\alpha$, $s\in\beta$. Thus $r'+s'\not\in\alpha+\beta$, whereby we see that $\alpha+\beta\neq\Q$. Thus, $\alpha+\beta$ has property (i).

  • Property (ii): Yes. Is $\alpha+\beta$ closed downward? Something to check. If $p\in\alpha+\beta$, say $q<p=r+s$, where $r\in\alpha$ and $s\in\beta$. We want to know whether or not $q\in\alpha+\beta$. Is $q\in\alpha+\beta$? What would it mean to show that $q$ is in $\alpha+\beta$? We would need to show that $q$ is the sum of two rational numbers, a rational number in $\alpha$ and a rational number in $\beta$. Now, we know $p$ is the sum of two rational numbers, namely $r$ and $s$, where $r\in\alpha$ and $s\in\beta$. Note that $q-s<r$ since, by supposition, we have $q<p=r+s$. Since $r\in\alpha$ and $q-s<r$, it must necessarily be the case that $q-s\in\alpha$ (since $\alpha$ is a cut). Then $q=(q-s)+s\in\alpha+\beta$, where $q-s\in\alpha$ and $s\in\beta$, as desired.

  Rudin: Pick $p\in\alpha+\beta$. Then $p=r+s$, with $r\in\alpha$, $s\in\beta$. If $q<p$, then $q-s<r$, so $q-s\in\alpha$, and $q=(q-s)+s\in\alpha+\beta$. Thus, property (ii) holds.

  • Property (iii): Yes. Is there no largest member? There is not---check this. My comment: Recall we most show that

    "If $p\in\alpha$, then $p<r$ for some $r\in\alpha$."

    in order for property (iii) to hold. Let $t\in\alpha$ and choose $t\in\alpha$ such that $t>r$. (We can make such a choice since $\alpha$ is a cut and thus has no largest element.) With $p=r+s$, where $r\in\alpha$ and $s\in\beta$, and $r<t$, we will certainly have $r+s<t+s$ or simply $p<t+s$, where $t+s\in\alpha+\beta$ since $t\in\alpha$ and $s\in\beta$. We may set $\eta=t+s$ in what follows to slightly simplify the conclusion.

    Recalling that $p\in\alpha+\beta$ (since $p=r+s$, where $r\in\alpha$ and $s\in\beta$), and $\eta\in\alpha+\beta$ (since $\eta=t+s$, where $t\in\alpha$ and $s\in\beta$), we see that we have shown the following:

    If $p\in\alpha+\beta$, then $p<\eta$ for some $\eta\in\alpha+\beta$.

    The above is what was required to show that property (iii) holds, and we have shown just that.

    Rudin: Choose $t\in\alpha$ so that $t>r$. Then $p<t+s$ and $t+s\in\alpha+\beta$. Thus, property (iii) holds.

  Since $\alpha+\beta$ satisfies properties (i)--(iii) for Dedekind cuts, we know that $\alpha+\beta$ is a cut. So we have an order, we have an addition. We would want to show that the axioms for addition A1--A5 all hold.

Do the addition axioms A1-A5 hold for cuts?

• Remark: We won't show all of these — we will just think through why they should be reasonable, and you can check them in your own privacy. Note that we showed A1 holds above by showing that $\alpha+\beta$ is a cut. We also showed that $Q_{-}$ is a cut, thereby showing $0^*=\Q_{-}$, where $0^*$ is defined below, is also a cut by definition. For instance what about commutativity?

• A2 (Commutativity): If we define $\alpha+\beta=\{r+s\mid r\in\alpha,s\in\beta\}$, then could we necessarily say that $\alpha+\beta=\beta+\alpha$? If so, why? Addition itself is commutative for rationals. So commutativity for reals follows from commutativity for rationals. This is nice.

  Rudin: $\alpha+\beta$ is the set of all $r+s$, with $r\in\alpha$, $s\in\beta$. By the same definition, $\beta+\alpha$ is the set of all $s+r$. Since $r+s=s+r$ for all $r\in\Q$, $s\in\Q$, we have $\alpha+\beta=\beta+\alpha$.

• A3 (Associativity): This is the same idea as that for commutativity.

  Rudin: As above, this follows from the associative law in $\Q$.

• A4 (Additive identity): What would the additive identity be? Let's give it a name. Let's call it zero but denote it as $0^*$ to remind ourselves that the additive identity in this case is not the rational number 0 but a collection. What should play the role of zero in this case? The set of all negative rationals makes sense (i.e., $0^*=\Q_{-}$) because if we take any rational number $r$ in $\alpha$, then adding a negative rational number $s$ to it will only make $r+s$ smaller than $r$, thus leaving $\alpha$ unchanged in the sense that $\alpha$ is a Dedekind cut and we "get all the rational numbers left of a cut location for free" in a sense. This gives us an intuitive understanding, but we should more formally check that adding any negative rational to a given rational in $\alpha$ leaves $\alpha$ unchanged; that is, we need to check that $\alpha+0*=\alpha$ as cuts; that is $\alpha+0^*$ and $\alpha$ are both sets of rational numbers and to show any two sets are equivalent we show that one contains the other or what is often called mutual subset inclusion. Symbolically, we should show that $\alpha+0^*\subset\alpha$ and $\alpha\subset\alpha+0^*$. If we can show this, then we will have shown that $\alpha+0^*=\alpha$. To start, we note that if we take anything in $\alpha$ and add something negative to it (i.e., something from $0^*$), then we will get back something in $\alpha$ because is $\alpha$ is closed downwards. This shows that $\alpha+0^*\subset\alpha$. Now let's go the other direction. Why is it that if I pick something in $\alpha$, then it's the sum of something in $\alpha$ plus something negative? Because there's no largest member of $\alpha$, let $p\in\alpha$, and then choose some $q\in\alpha$ such that $p<q$ and $p=q+(p-q)$. Since $p<q$, we have $p-q<0$, whereby it becomes clear that $p=q+(p-q)$ is an element of $\alpha+0^*$ since $q\in\alpha$ and $(p-q)\in 0^*$. Since we have just shown that $p\in\alpha$ implies $p\in\alpha+0^*$ for arbitrary $p$, it is clear that $\alpha\subset\alpha+0^*$. We thus conclude that $\alpha+0^*=\alpha$.

  Rudin: If $r\in\alpha$ and $s\in 0^*$, then $r+s<r$, hence $r+s\in\alpha$. Thus $\alpha+0^*\subset\alpha$. To obtain the opposite inclusion, pick $p\in\alpha$, and pick $r\in\alpha$, $r>p$. Then $p-r\in 0^*$, and $p=r+(p-r)\in\alpha+0^*$. Thus $\alpha\subset\alpha+0^*$. We conclude that $\alpha+0^*=\alpha$.

• A5 (Additive inverse): This is a little more complicated. On the surface, it's not quite clear what the inverse of $\alpha$ should be. Here is a definition that is rather unmotivated at the moment, but it will make sense upon some reflection. Our set $\beta$ will consist of all rationals $p$ such that there exists a number $r>0$ such that $-p-r\not\in\alpha$. In symbols:

  $$\beta=\{p\mid \exists r>0\ \text{such that}\ -p-r\not\in\alpha\}.$$

  Our job, then, is to show that $\alpha+\beta=0^*$.

  Rudin: Rudin's exposition is rather involved. First he shows that $\beta$ actually is a cut. And then he appeals to the archimedean property of $\Q$ later on. See [5] for an analysis as well as Bergman's errata. This is definitely the most involved proof for A1-A5. Note that Su gives somewhat of a hand-wavy explanation at the end of A5, but it may be worth revisiting once Bergman has been read and fleshing out the illustration in more detail.

Do the multiplication axioms M1-M5 hold for cuts?

• Comments: We'll just make a few comments since it is rather much so what you would expect. Addition is the sum of two things, one from one cut and one from another cut. We would like to define multiplication as the product of two things, where we multiply one thing from one cut by another thing from another cut. The only problem with that is if we have some negatives, then we run into a few problems, since products of negative rationals are positive.

• Definition: If $\alpha,\beta\in\R_+$ (i.e., $\alpha,\beta>0^*$), then

  $$\alpha\beta=\{p\mid p<rs\ \text{for some}\ r\in\alpha,s\in\beta, r,s>0\}.$$

  We will then let $1^*=\{q<1\mid q\in\Q\}$. For negative reals, see Rudin. (Basically, you make them positive, you multiply, then you negate as needed.) The claim is that our definition of multiplication satisfies the axioms of multiplication M1-M5.

Do cuts have suprema?

• Supremums of cuts: How would you take the supremum of a bunch of cuts? A hint is to look at a collection of a whole bunch of cuts and ask ourselves what the cut is that will be the cut that contains all of the cuts in our collection because it is bigger but it's the smallest cut that contains them all? We essentially want the supremum to be the union of the bunch or collection of cuts — this is a beautiful description of what the supremum ought to be. Given a bunch of cuts, $A$, let $\gamma$ be the union of all the $\alpha$ where $\alpha\in A$; that is, given a collection of cuts $A$, let

  $$\gamma=\bigcup_{\alpha\in A}\alpha.$$

  Our claim is that $\gamma$ will be a cut and that $\gamma=\sup A$. It should be clear that $\gamma$ is an upper bound (because it contains everything), but why it is a least upper bound we shall see next time. Once we do that, we'll have very easily shown that $\R$ has this property that $\Q$ does not have. The set $\R$ is "complete." It has all its holes filled in.

Thoughts and questions

• Look more into the construction of the real numbers, particularly the construction via Cauchy sequences at some point. It looks like Dedekind's approach is quite popular due to the fact that he only uses tools available to us from an early time period. That is, for example, the Cauchy sequence approach requires that we use (shock) Cauchy sequences, a tool that is not available until later.
• How might one construct the integers? See [13].
• How might one construct the natural numbers? See [12].