15 - Convergence of sequences

Where we left off last time

We have spent a lot of time developing properties of compactness and understanding it as a finiteness condition. Today we want to start talking about sequences, and so this will actually bring us to the developing concepts like continuity, continuous functions, what does it mean for a function to be continuous — that's defined in terms of limits. And so we have to say what it means to take the limit of a sequence. Where do we start?

• Correction from previous lectures: Recall that one way of characterizing compactness was by the finite intersection property. Here is the proper statement:

  Finite Intersection Property. A collection of sets has the finite intersection property if every finite subcollection has non-empty intersection.

  Previously, the above statement was coupled with a result characterizing compactness even though this result should have been omitted from the property statement. The characterization of compactness can be expressed as follows:

  A set is compact if and only if every collection of closed sets $\{K_\alpha\}$ that has the finite intersection property has non-empty intersection; that is, $\bigcap_{\alpha} K_\alpha\neq\emptyset$.

  So we're demanding that we only look at collections that have the finite intersection property. Because there certainly could be some collections that don't, namely take two disjoint closed sets. Certainly they would not satisfy the finite intersection property, and I'd be demanding nothing about them.

Sequences

What are sequences and what's the main idea behind them?

• Recall and definitions: We've actually encountered sequences before when we started talking about countable sets. We said okay well can we list the set in a sequence. So really what is a sequence? A sequence $\{p_n\}$ in some metric space $X$ is a function $f\colon\N\to X$ (This is a function that goes from the natural numbers to some point in $X$.) defined by $n\mapsto p_n$, where $p_n$ is a point in $X$. We are doing this in the general context of metric spaces because we want to refrain from only thinking about sequences of real numbers. At some point, we'd like to think about, say, sequences of functions or the like. If you were a physicist or an engineer, then you'd be interested in wave forms and whether or not they converged as a sequence. Let's address some potential issues with sequences. We might have, for instance, the plane which is a metric space where we have the Euclidean metric, and we'd like to know what a sequence looks like, especially possibly the idea of "convergence."

• Example 1: Consider the following picture:

  

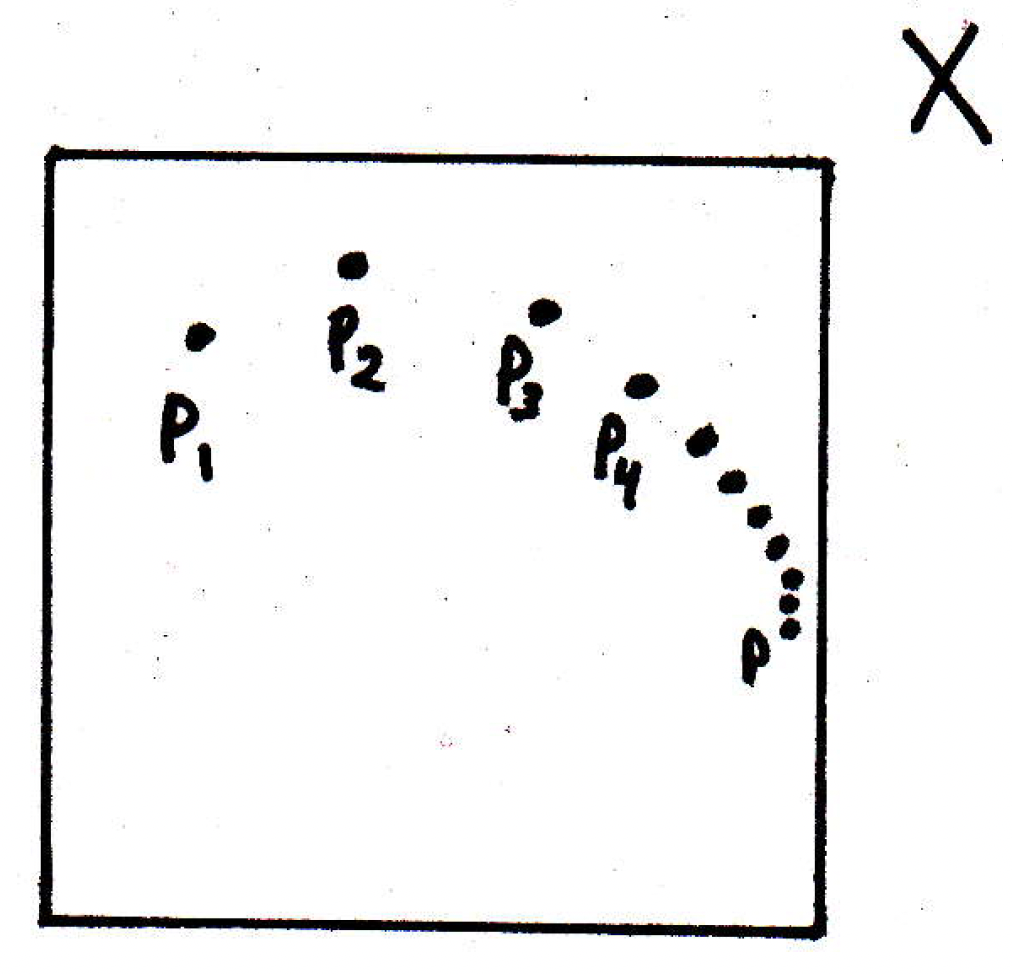
  We have a bunch of points "moving around" in a metric space $X$ above, and it looks like the sequence is actually doing something. The picture above is just a schematic of points in the plane, but we could also be talking about points in a space of functions where each of the points above is a function and asking whether or not those things converge. So that's the real question: What does it mean for a sequence to converge? It's easy to bring a lot of tuition to this discussion, but our goal will be to precisely pinpoint exactly what it means for a sequence to converge. If we think about the word "convergence" rather informally, then it makes sense to talk about the sequence in the picture above as "converging" to a point $p$ perhaps because "the points are getting closer to something," namely the point $p$ listed in the picture above. We wouldn't say that the sequence also converges to the point $q$ pictured below:

  

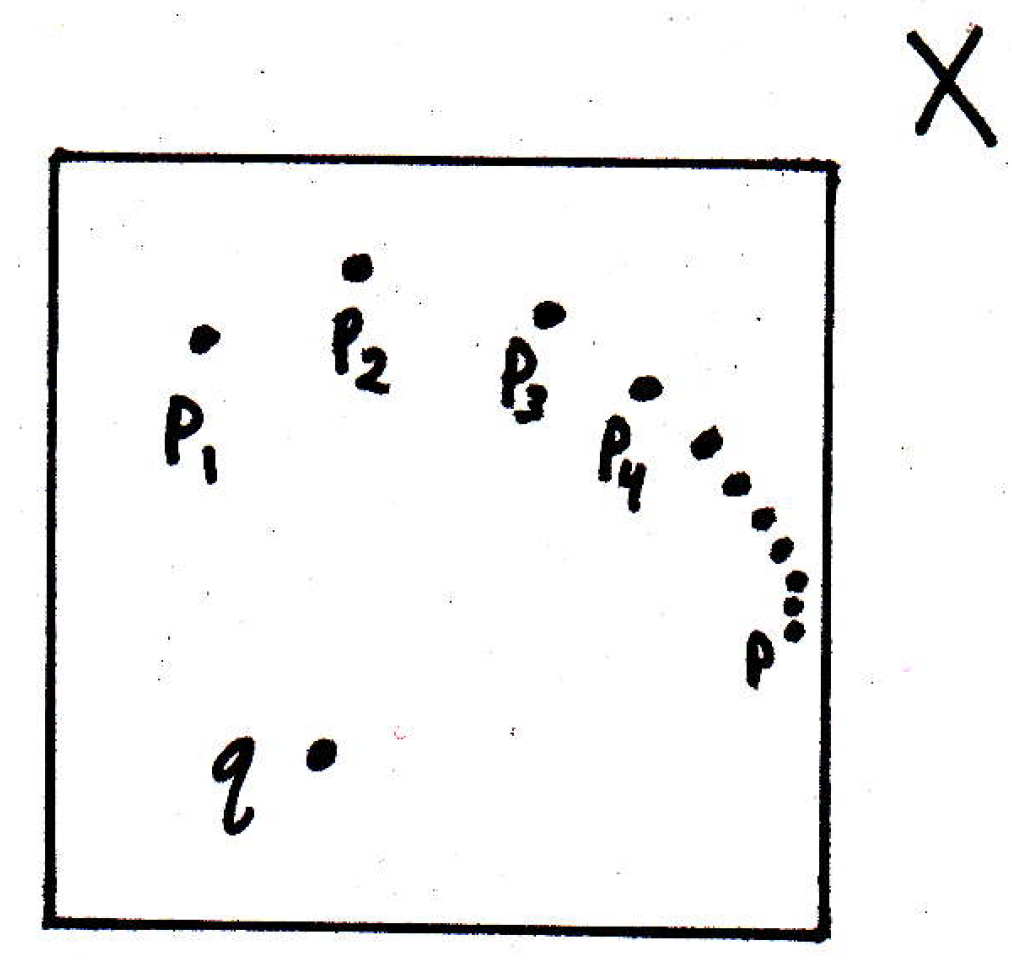
  Why wouldn't we say our sequence converges to $q$? Well, the points are do not seem to be getting closer or nearer to $q$, and the notion of "nearness" is important, and a metric here is going to be rather important.

• Example 2: Consider the following picture:

  

  Would we say the sequence pictured above (where the sequence keeps going in both directions) converges in the plane? It doesn't seem like there's any point that the points are "narrowing in on." It certainly does not seem like such a sequence converges in any meaningful way.

• Example 3: Consider the following picture where every point is the same:

  

  Would we say the sequence above converges? Seems relatively reasonable to say such a sequence converges. And we'd just say it converges to $p$.

• Example 4: Consider the following picture:

  

  We have a ton of different points where we are just going back, forth, back, forth, back, forth, etc. Does such a sequence converge? No, it certainly does not seem to be so.

• Convergence (motivating definition): The right notion of convergence should capture the idea that "points beyond a certain place" should be getting closer to something. For the examples above, it seems like we would say that Examples 1 and 3 have convergent sequences whereas Examples 2 and 4 do not, whatever that means. We are still going to try to make this concept very precise. So let's try to formulate a definition. Based on the examples, what's true of examples 1 and 3 that's not true of examples 2 and 4?

• Convergence (definition): The sequence $\{p_n\}$ converges if there exists a point $p\in X$ such that for any $\epsilon>0$ there exists a number $N$ such that $n\geq N$ implies $d(p_n,p)<\epsilon$. We may write this as follows for ease of reference:

  $$(\forall\epsilon>0)(\exists N)(n\geq N\implies d(p_n,p)<\epsilon). \tag{1}$$

  If the requirements in (1) are met, then we say that $\{p_n\}$ converges to $p$, or that $p$ is the limit of $\{p_n\}$, and we write $p_n\to p$, or

  $$\lim_{n\to\infty}p_n=p.$$

  If $\{p_n\}$ does not converge, then it is said to diverge. Note that in this definition $N$ is an index. We are saying that $N$ is the number beyond which all of the terms of $\{p_n\}$ are within $\epsilon$ of $p$.

• Illustration of definition: For Example 1, you can give me any $\epsilon>0$, and it will be a ball around $p$, where our goal is to communicate that there is a point in the sequence beyond which all the terms are inside the $\epsilon$-neighborhood. The sample applies for Example 3:

  

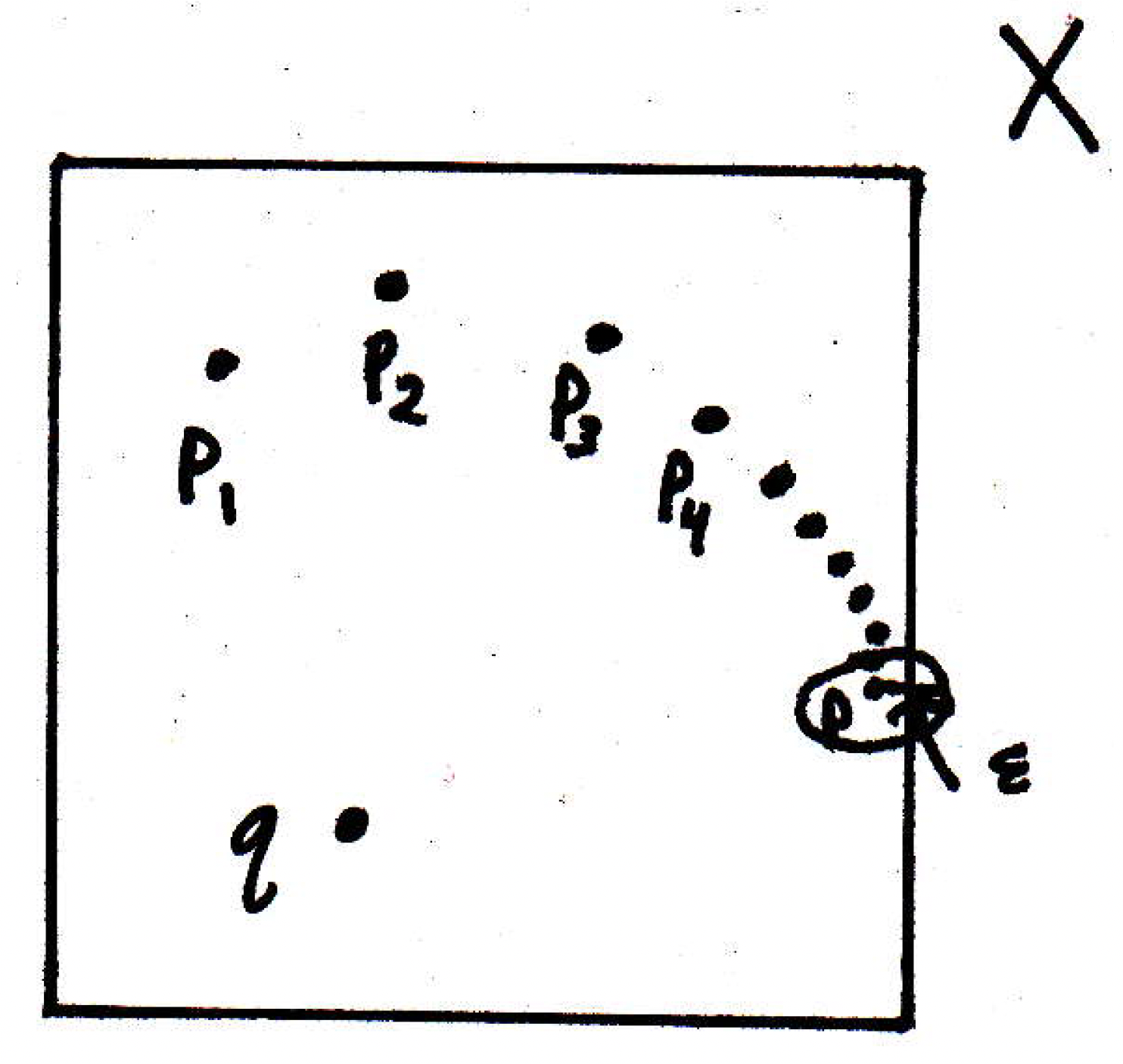
  The sample applies for Example 3:

  

  What about something like the following picture:

  

  It certainly looks like the sequence is converging to a point $p$ eventually even though it jumps up to $p_{10}$ in a seemingly random fashion, and it also jumps back up to $p_{13}$ randomly as well. The "jumping around" piece is not really a problem here though. Why? Well, if we jumped up outside of the $\epsilon$-neighborhood at $p_{1000}$, then we would simply go $p_{1001}$.

• Limits and limit points: Given our definition of what it means for a sequence to converge, which namely involves the notation

  $$\lim_{n\to\infty}p_n=p,$$

  we may ask ourselves what the connection is between the sequence converging and limit point. What's the connection? We'll see it in a second.

• Example of convergent sequence: How about the sequence

  $$p_n=\frac{n+1}{n}$$

  in the metric space $\R$? Does it converge? Based on our experience with other math and maybe just some intuition, we might say this seems it converges to 1, not 10 or something else. Can we prove it though? We claim $p_n\to 1$. If we're going to actually prove this using the definition of what it means for a sequence to converge, then what must we show? To establish convergence, our task is to, given an epsilon greater than zero, to find an $N$ that works (i.e., so that the requirements in (1) are fulfilled), and this is how this kind of proof pretty much always works. Now, how are we going to measure distance in the real line? Take the absolute value of the difference. So we're trying to find some $N$ such that $d(p_n,p)<\epsilon$ or, using the Euclidean metric, $|p_n-p|<\epsilon$. If we suspect that $\{p_n\}$ converges to 1, where $p_n=\frac{n+1}{n}$, then we need to somehow bound the difference:

  $$\biggl|\frac{n+1}{n}-1\biggr|<\epsilon.$$

  Right now we're kind of just working backwards. (This is how most proofs are actually cobbled together even though the logical presentation thereafter will often differ substantially in how ideas were encountered.) The question we should be asking ourselves at this juncture is when is it the case that $|\frac{n+1}{n}-1|<\epsilon$? For which $N$? That's what we're trying to find here. An equivalent question is asking when $|\frac{1}{n}|<\epsilon$, and this occurs when $n>\frac{1}{\epsilon}$. So now we have some sort of understanding when this bound holds. To bring this back around to our definition, is there a point in the sequence $p_n=\frac{n+1}{n}$ beyond which the condition $\frac{1}{\epsilon}<n$ always holds? What should $N$ be? How about anything greater than $\frac{1}{\epsilon}$? Then, if $n\geq N$, then we will have our desired conclusion. Let's give a concrete proof now.

  Given $\epsilon>0$, let $N=\lceil \frac{1}{\epsilon}\rceil$, where we have chosen the ceiling function just to ensure that we have a natural number to coincide with the term number of our sequence (recall $N$ is an index and should have natural number values since a sequence is a function with domain $\N$ and codomain $X$). If $n\geq N$, then $n\geq\frac{1}{\epsilon}$; hence, $\frac{1}{n}\leq\epsilon$. Sp $|p_n-p|=|\frac{n+1}{n}-1|=|\frac{1}{n}|\leq\epsilon$.

  We would like the inequality above to be strict. How can we fix it? We could set $N=\lceil \frac{1}{\epsilon}\rceil+1$. Then, if $n\geq N$, then we certainly have $n>\frac{1}{\epsilon}$; hence, $\frac{1}{n}<\epsilon$. So then $|p_n-p|=|\frac{n+1}{n}-1|=|\frac{1}{n}|<\epsilon$, as desired.

• True or false (statements): Try to mark the following as true or false:

  1. If $p_n\to p$ and $p_n\to p'$, then $p=p'$.
  2. If $\{p_n\}$ is bounded, then $p_n$ converges. (By saying "$\{p_n\}$ is bounded" we mean if we look at $\{p_n\}$ as a function, then its range is bounded or simply that all of the points that it achieves lie in some ball).
  3. If $p_n$ converges, then $\{p_n\}$ is bounded.
  4. If $p_n\to p$, then $p$ is a limit point of the range of $\{p_n\}$.
  5. If $p$ is a limit point of $E$ in $X$, then there exists $\{p_n\}$ in $E$ such that $p_n\to p$.
  6. If $p_n\to p$, then every neighborhood of $p$ contains all but finitely many $p_n$.

• True or false (answers/discussions): Discuss the above statements and whether or not they are true or false.

  1. If $p_n\to p$ and $p_n\to p'$, then $p=p'$.

  Discussion: True. Why? There is some fixed distance between $p$ and $q$, and let's call this distance $\epsilon$, and we can focus on a distance $\frac{\epsilon}{2}$. When we apply the definition of convergence, we are talking about any epsilon we like. This will cause some problems here. How can we make a contradiction precise? After some point in the sequence, say after the 17th term, all terms are in the $\frac{\epsilon}{2}$-ball of $p$. But we could also draw a $\frac{\epsilon}{2}$-ball around $q$. And after some point in the sequence, say the 52nd term, all terms are in the $\frac{\epsilon}{2}$-ball around $q$. Where is the contradiction? Well, if we take the bigger of 52 and 17, then all of the terms have to be in both balls, but both balls are disjoint, which can be proven by the triangle inequality. So we are in good shape.

  More precisely, assume $p_n\to p$ and $p_n\to q$. Let $\epsilon=d(p,q)$, where we will assume $p\neq q$, and hence $\epsilon>0$. (A proof by contradiction is coming.) Then there exists $N_p$ such that $n\geq N_p$ implies $d(p_n,p)<\frac{\epsilon}{2}$. Also, there exists $N_q$ such that $n\geq N_q$ implies $d(p_n,q)<\frac{\epsilon}{2}$. Let $N=\max\{N_p,N_q\}$. Then $n\geq N$ implies that $\epsilon=d(p,q)\leq d(p,p_n)+d(p_n,q)<\frac{\epsilon}{2}+\frac{\epsilon}{2}$, a contradiction.

  2. If $\{p_n\}$ is bounded, then $p_n$ converges. (By saying "$\{p_n\}$ is bounded" we mean if we look at $\{p_n\}$ as a function, then its range is bounded or simply that all of the points that it achieves lie in some ball).

  Discussion: False. Recall Example 4 from before where we had points jumping back and fourth. The points we contained in some ball, but they definitely did not converge.

  3. If $p_n$ converges, then $\{p_n\}$ is bounded.

  Discussion: True. We may have a picture of a sequence $\{p_n\}$ such as the following:

  

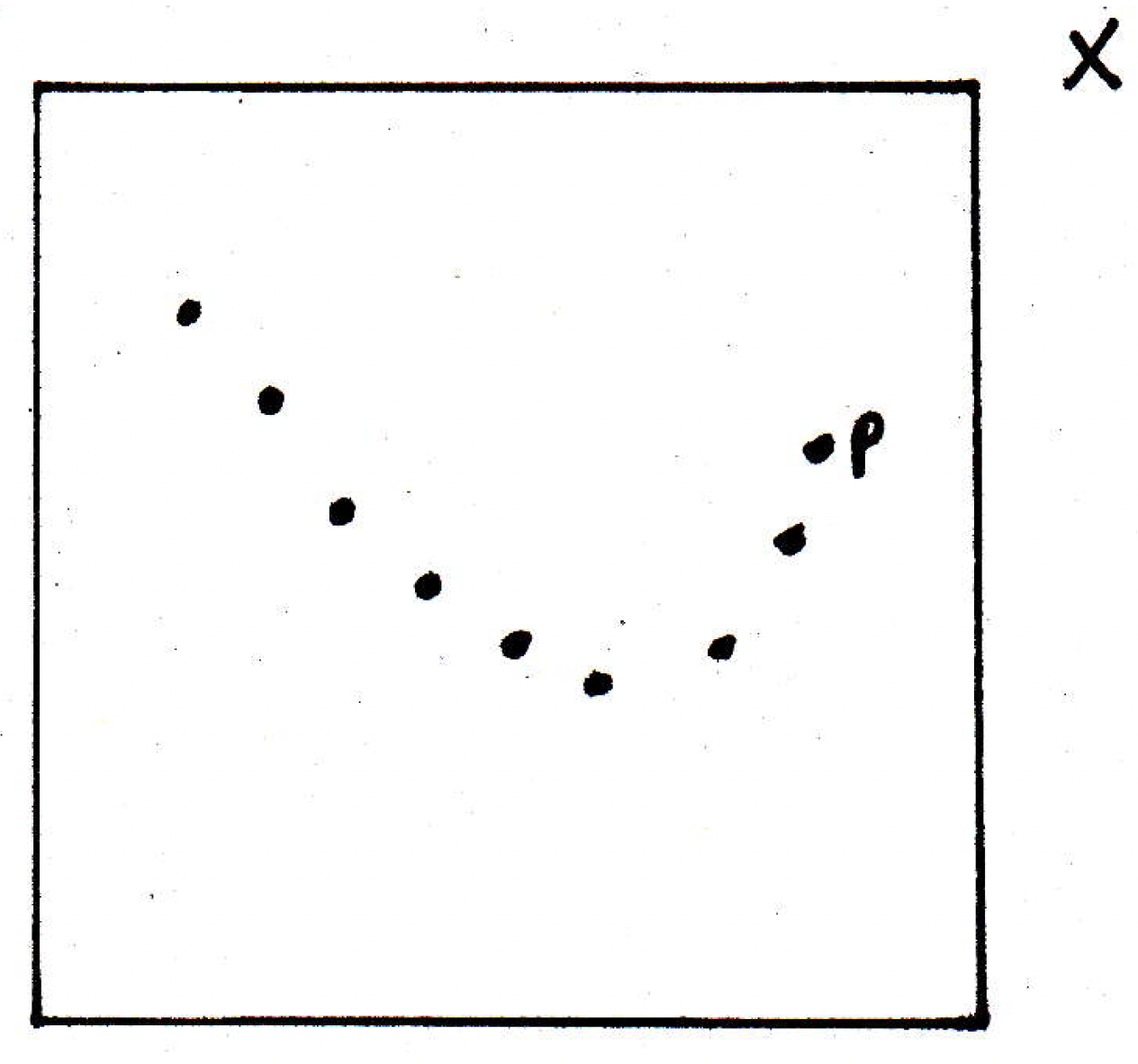
  Since $\{p_n\}$ converges to some point, say, $p$, then we really will have a picture that looks something like the following, where for any $\epsilon$ there is a point beyond which all points are inside the ball:

  

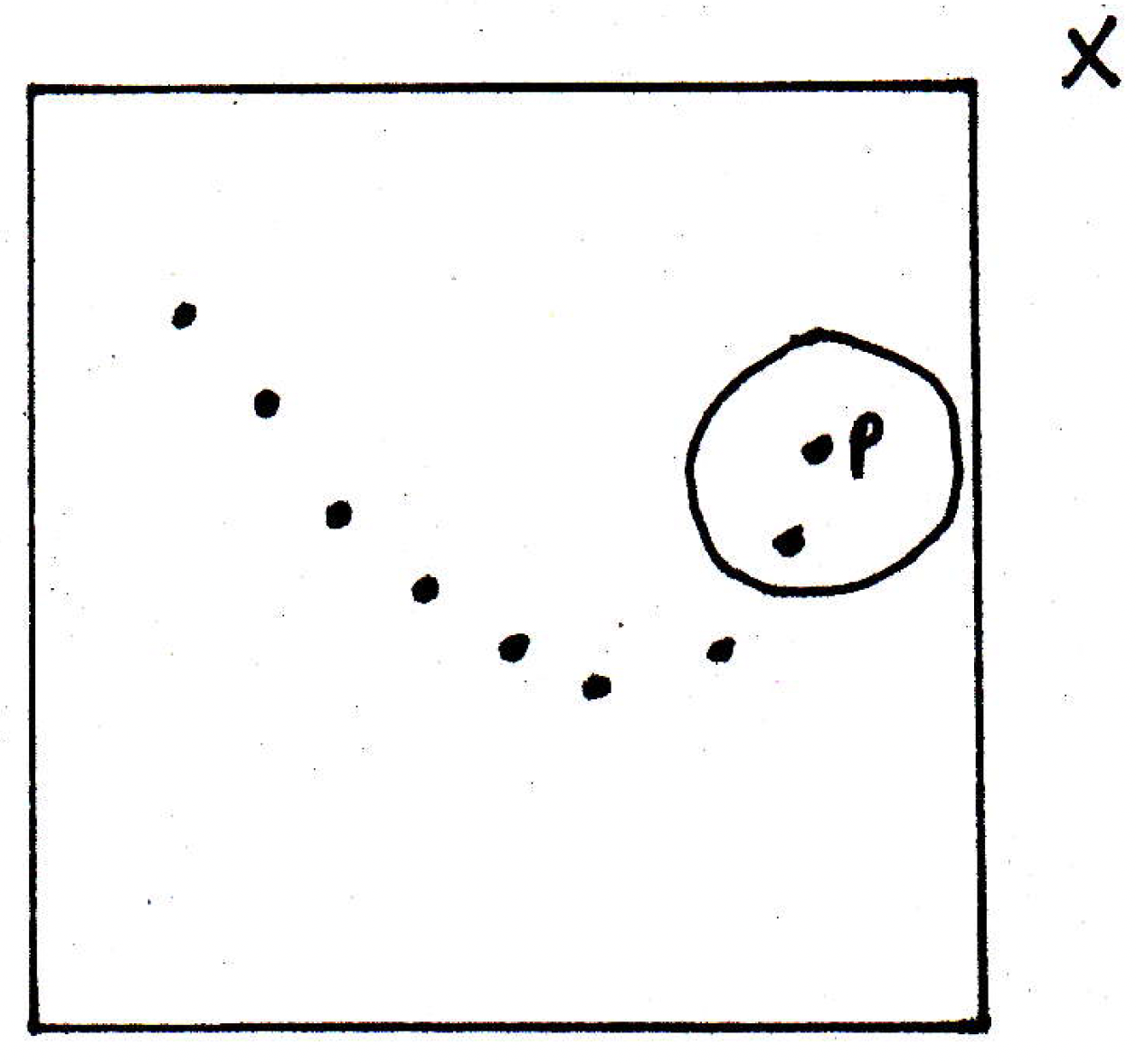
  How is this significant? Why does $\{p_n\}$ have to be bounded? Well, beyond some term of the sequence, say the 47th term, all of the sequences are then in the ball. So how many other points are there outside of the ball? Finitely many. That's the basic idea.

  Use $\epsilon=1$, then there exists $N$ such that $n\geq N$ implies $d(p_n,p)<1$. Let $R=\max\{1,d(p,p_1),\ldots,d(p,p_{N-1})\}$. So all $\{p_n\}$ are in some ball $B_{R}(p)$. 4. If $p_n\to p$, then $p$ is a limit point of the range of $\{p_n\}$.

  Discussion: False. Example 3 considered previously is a problem. If all of the points are the same, then a point sitting on top can't be its own limit point of its range. So while the concepts are related, they're not exactly the same. We have that $p$ is the limit of $p_n$ but $p$ is not a limit point of the range of $\{p_n\}$ as indicated in Example 3. Limits and limit points are different. They're related concepts but different. Why are they related? Look at the statement below.

  5. If $p$ is a limit point of $E$ in $X$, then there exists $\{p_n\}$ in $E$ such that $p_n\to p$.

  Discussion: True. Why? Consider the following picture:

  

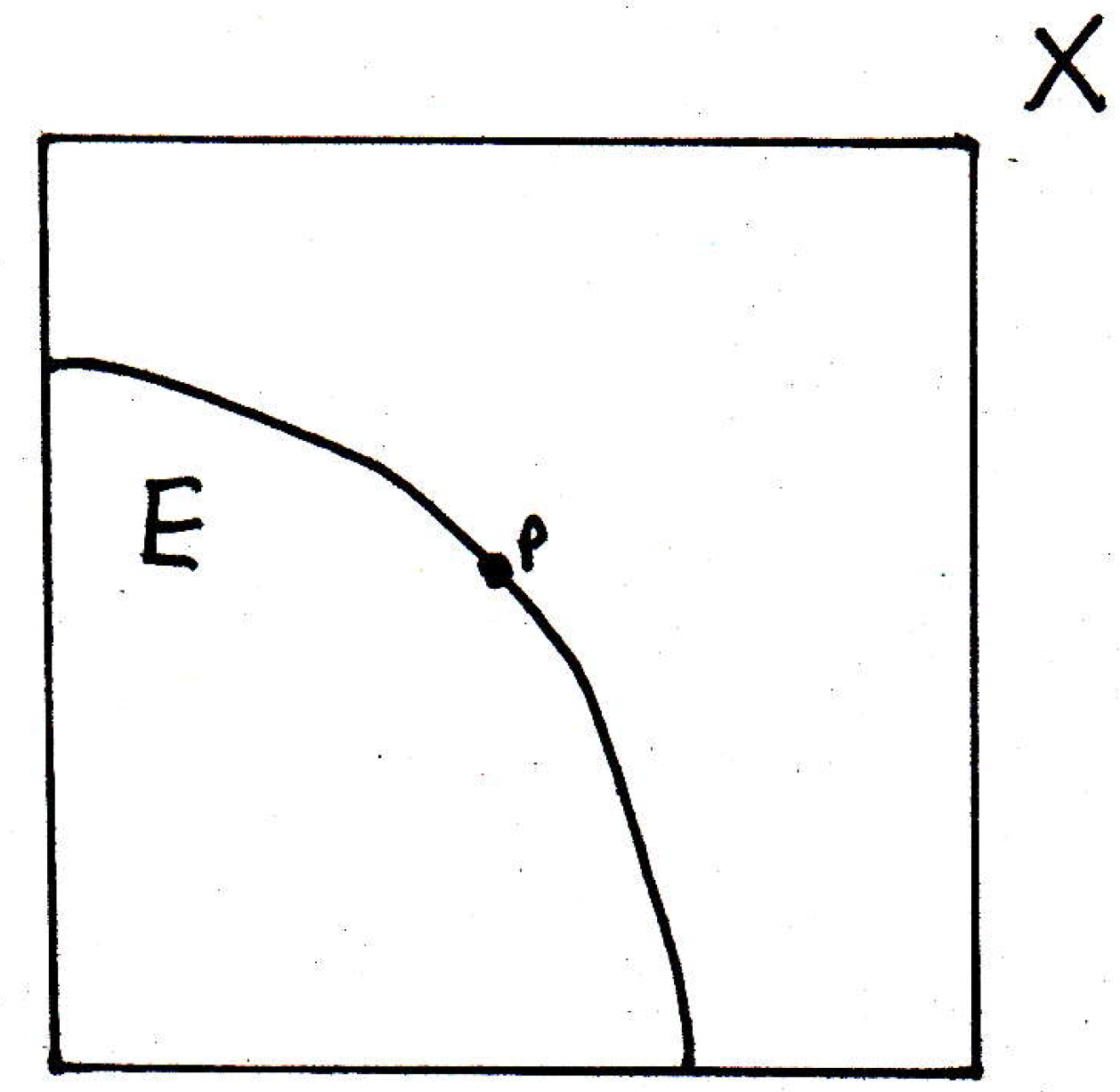
  How can we find a sequence $\{p_n\}$ in $E$ that converges to $p$? Well, if $p$ is a limit point of $E$, then we can envision a picture like the following:

  

  The picture above was constructed by first picking a ball of radius, say $\frac{1}{2}$, around $p$. Since $p$ is a limit point of $E$, then this ball has to contain a point $q\neq p$ such that $q\in E$. Okay. Now we pick a ball of radius $\frac{1}{3}$ around $p$ for which we get another point in $E$. And so forth. By doing this, we get a sequence of points that must converge to $p$. That's the idea.

  So choose a sequence $p_n\in B_{\frac{1}{n}}(p)$. Then $p_n\to p$. (Try to justify this — it follows from how we've chosen the points of $\{p_n\}$.)

  6. If $p_n\to p$, then every neighborhood of $p$ contains all but finitely many $p_n$.

  Discussion: True. Return to the following picture:

  

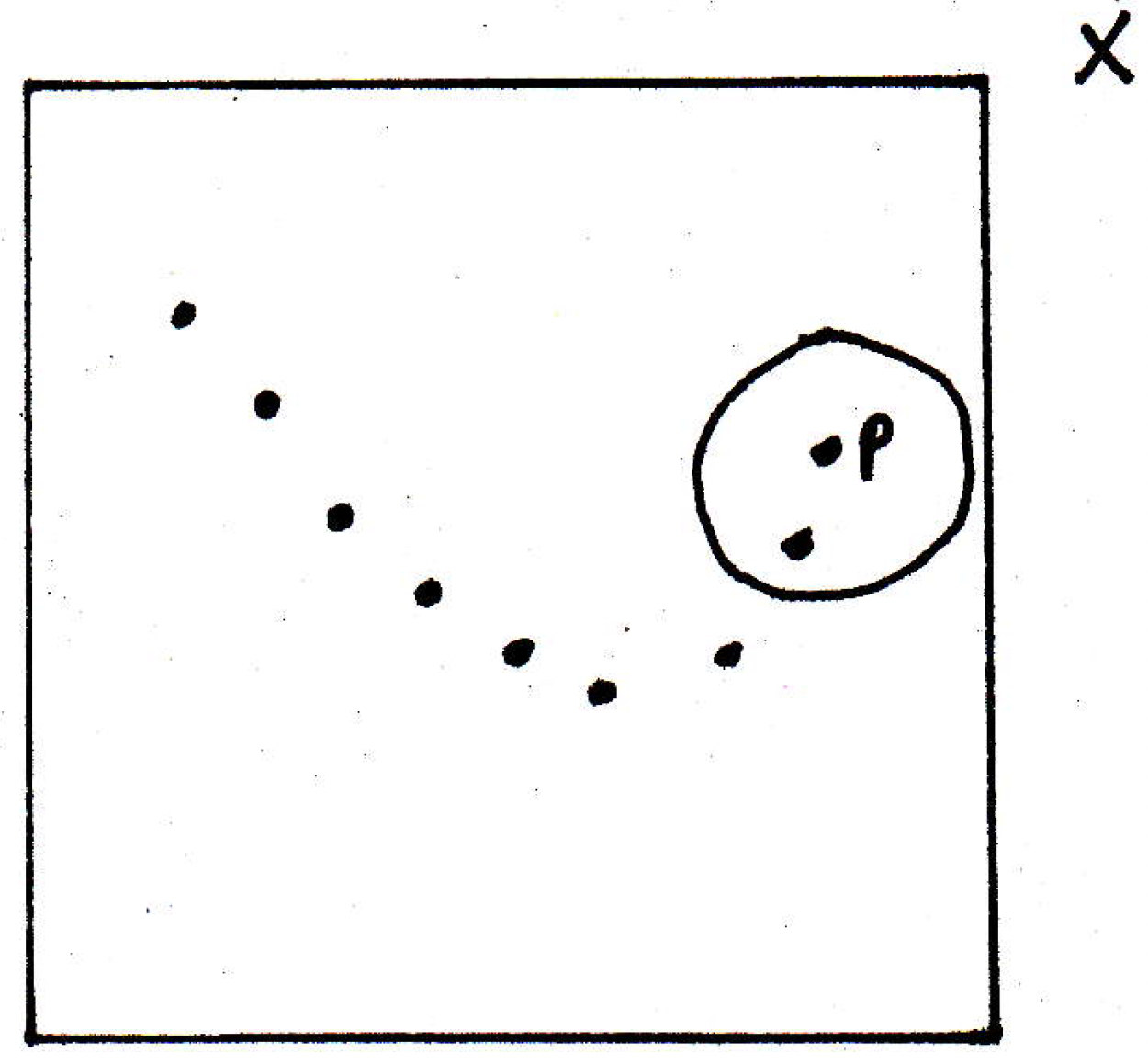
  It sort of gives the idea. Everything is in the ball and everything else is out. The forward direction is true due to (1). It turns out that the reverse direction is true also. If every neighborhood of $p$ contains all but finitely many $p_n$, then we claim that we must have $p_n\to p$. Why? Well, according to (1), you have to find me a $N$ for every $\epsilon$. Basically, if it contains all but $p_1,\ldots,p_{47}$, then we will let $N=47$. So this means the converse is also true.

• Next time: We've talked a fair amount about sequences in a metric space $X$. Next time, we will talk about sequences in $\R$ and $\R^n$, and we will think about what we can say about their convergence. For instance, if you take a limit of a sequence in $\R$, then you can talk about summing two sequences. Is the limit of a sum the sum of the limits? Is the limit of a product of sequences the product of the limits?